Курсовая работа: Системы эквивалентные системам с известным типом точек покоя
 , если с
, если с![]() 0;
0;
x=0, y=at+c![]() , если с=0, где постоянные с, с
, если с=0, где постоянные с, с![]() , с
, с![]() связаны соотношением с
связаны соотношением с![]() (b+c
(b+c![]() +c
+c![]() )=a
)=a![]() , имеет два центра в точках
, имеет два центра в точках![]()
![]() и
и ![]() .
.![]()
Решение:
Подставим общее решение
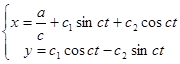 в нашу систему (1) получим
в нашу систему (1) получим 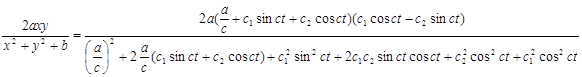
![]()
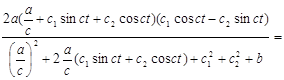
=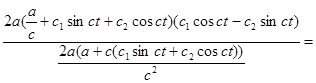
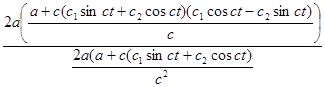 =c(c
=c(c![]() cosct-c
cosct-c![]() sinct)=
sinct)=![]()
a-![]()
![]()
Для краткости распишем знаменатель и преобразуем
x![]() +y
+y![]() +b=
+b=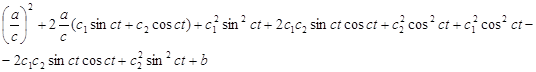
![]()
![]() =
=![]()
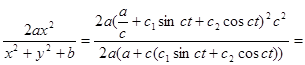
![]()
=a+c(c![]() sinct+c
sinct+c![]() cosct)
cosct)
a-![]()
![]()
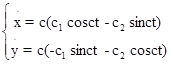
Получаем, что x и y являются общим решением системы.
3. Нахождение первого интеграла дифференциальной системы и условия его существования
Рассмотрим систему ![]() = f (t, x), x= (x
= f (t, x), x= (x![]() ,…, x
,…, x![]() ), (t, x)
), (t, x)![]() (1) с непрерывной в области D функцией f. Дифференцируемая функция U (t, x), заданная в некоторой подобласти G области D, называется первым интегралом системы (1) в области G, если для любого решения x(t), t
(1) с непрерывной в области D функцией f. Дифференцируемая функция U (t, x), заданная в некоторой подобласти G области D, называется первым интегралом системы (1) в области G, если для любого решения x(t), t![]() , системы (1), график которого расположен в Gфункция U (t, x(t)), t
, системы (1), график которого расположен в Gфункция U (t, x(t)), t![]() , постоянна, т.е. U (t, x(t)) зависит только от выбора решения x(t) и не зависит от t.
, постоянна, т.е. U (t, x(t)) зависит только от выбора решения x(t) и не зависит от t.
Пусть V (t, x), V:G![]() R , есть некоторая функция. Производной от функции V в силу системы (1) назовем функцию V
R , есть некоторая функция. Производной от функции V в силу системы (1) назовем функцию V![]() V
V![]() R, определяемую равенством
R, определяемую равенством
V![]() (t, x(t))
(t, x(t))![]() t
t![]() .
.
Лемма 1.
Для любого решения x(t), t![]() , системы (1), график которого расположен в G, имеет место тождество
, системы (1), график которого расположен в G, имеет место тождество
V![]()
![]() t
t![]() .
.
Без доказательства.
Лемма 2.
Дифференцируемая функция U (t, x), U:G![]() R , представляет собой первый интеграл системы (1) тогда и только тогда, когда производная U
R , представляет собой первый интеграл системы (1) тогда и только тогда, когда производная U![]() в силу системы (1) тождественно в G обращается в нуль.
в силу системы (1) тождественно в G обращается в нуль.
Необходимость. Пусть U (t, x) есть первый интеграл системы (1). Тогда для любого решения x(t) этой системы, применяя лемму 1 будем иметь тождества
U![]()
![]()
![]()
Откуда при t=t![]() получим равенство U
получим равенство U![]() (t
(t![]() справедливое при всех значениях t
справедливое при всех значениях t![]() и x(t
и x(t![]() ). Необходимость доказана.
). Необходимость доказана.