Курсовая работа: Системы эквивалентные системам с известным типом точек покоя

[в нашем случае ] = =[учитывая все сделанные обозначения] =

=

=

=[ввиду того, что которое в свою очередь как мы уже показали есть тождественный ноль]

Таким образом, тождество (3) истинное.

4. Отражающая функция

Определение. Рассмотрим систему

(5)

cчитая, что правая часть которой непрерывна и имеет непрерывные частные производные по . Общее решение в форме Коши обозначено через ). Через обозначим интервал существования решения .

Пусть

Отражающей функцией системы (5) назовём дифференцируемую функцию , определяемую формулой

Для отражающей функции справедливы свойства:

1.) для любого решения системы (5) верно тождество

2.) для отражающей функции F любой системы выполнены тождества

3) дифференцируемая функция будет отражающей функцией системы (5) тогда и только тогда, когда она удовлетворяет системе уравнений в частных производных

и начальному условию

5. Применение теоремы об эквивалентности дифференциальных систем

Получаем где - любая нечетная непрерывная функция.

Наряду с дифференциальной системой 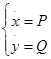(1)

рассмотрим возмущенную систему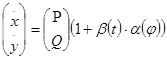(2), где - любая непрерывная нечетная функция. Известно по [3], что дифференциальная система (3)

эквивалентна возмущенной системе

(4), где непрерывная скалярная нечетная функция удовлетворяющая уравнению