Курсовая работа: Системы эквивалентные системам с известным типом точек покоя

а с ним и достаточность.

Из определения первого интеграла следует, что постоянная на G функция также является первым интегралом системы (1). Первый интеграл U (t, x) будем называть на G, если при всех (t, x) выполняется неравенство.

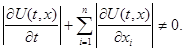
Функцию U(x) будем называть стационарным первым интегралом системы (1), если она не зависит от t и является первым интегралом системы (1).

Найдем первый интеграл нашей системы:

Возведем в квадрат и выразим с

y

Положим , получим

Проверим, что функция – это первый интеграл системы (1), т.е. проверим выполнение тождества (2)

Найдем производные по t, x, y

После выше сделанных преобразований получаем, что функция – это первый интеграл системы (1),

2) Положим , т.е. ,

где , Q

3) Проверим выполнение тождества:

(3), где