Курсовая работа: Составление теоретической конструкции балки

Отсюда, учитывая что Mmax = – 3 qa2,

[σ]=,

σвр=, Fте находим из диаграммы растяжения

σвр = = 318 МПа,

[n] = 1,5 если > 5%, [n] = 2,4 если < 5%,

= =0,7%,

[σ] = 318/2,4=132,5 МПа, отсюда Wx ≥ Mmax/ [σ]=60,48∙103/132,5∙106 = 456 см3.

Условиям прочности удовлетворяет Wx ≥ 456 см3

Согласно условиям жесткости

≤ [f],

откуда l/[f] = 900, [f] = l/900 =2,5/900 = 2,8 мм

Ix ≥== 4608 см4;

Учитывая условия прочности и жесткости по ГОСТу 8510-86 выбираем неравнобокие уголки №27 с следующими параметрами:

B=250мм, b=160 мм, d=18мм, A=157 см2, Ix=4987см4, Wx=597,6см3.

3 Другие элементы

3.1 Раскрытие статической неопределимости

Данная система дважды статически неопределима (две дополнительные связи), поэтому канонические уравнения имеют вид:

Коэффициенты при неизвестных, увеличенные в EI раз:

Проверка:

Свободные члены, увеличенные в EI раз:

;

Проверка: ;

Канонические уравнения имеют вид:

3.2 Определение опорных реакций

3.3 Построение эпюр внутренних силовых факторов

Эпюра Q. Эпюра строится по формуле . Вычисляем значения Q в характерных точках:

и строим эпюру Q.

Эпюра M. Эпюра строится согласно выражению

.

Эпюра N. Деформацию сжатия испытывают стержни BC и CD. Продольная сила в пределах каждого участка постоянна и принимает следующие значения:

3.4 Проверка решения

3.4.1Статическая проверка

Узел B

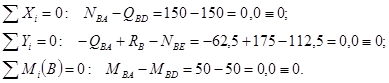
Узел C

3.4.2 Кинематическая проверка. Проверка состоит в выполнении условия

.

4 Расчет нагрузки на элементы

4.1 Определение геометрических характеристик сечения

а)Координаты центра тяжести.

№ п/п	vi	Ai	vi Ai
1	10t	32t2	320t3
2	4t	16t2	64t3
Σ		48t2	384t3

uc=0, vc==384t3/48t2=8t.

б) Моменты инерции относительно главных центральных осей x, y.

Предварительно вычисляем осевые моменты инерции отдельных частей относительно собственных центральных осей ξiηi

I= 8t·(4t)3/12 = 42,67t4,

I= 2·t·(8t)3/12 = 85,33t4,

I= 4t·(8t)3/12 = 170,67t4,

I= 2·8t·t3/12 = 1,33t4.

Остальные вычисления представим в табличной форме.

№ п/п	xi	yi	Ai	Ix=Σ(I+Ai)			Iу=Σ(I+Ai)
				I	Ai	I	I	Ai	I
1	0	2t	32t2	42,67t4	128t4	213,33t4	1,33t4	0	1,33t4
2	1,5t	-4t	16t2	85,33t4	256t4	298,67t4	170,67t4	36t4	206,67t4
Σ			48t2	128t4	384t4	512t4	172t4	36t4	208t4

в) Главные радиусы инерции

ix2 = Ix/A = 512t4/(48t2) = 10,67t2;

iy2 = Iy/A = 208t4/(48t2) = 4,33t2.

Построение ядра сечения. Для фигуры с прямолинейными сторонами ядро сечения представляет собой выпуклый многоугольник, координаты вершин которого определяются формулами:

xяi= – iy2/ai , yяi= – ix2/bi .

Здесь ai и bi – отрезки, отсекаемые нейтральной линией на осях координат, при ее обкатывании вокруг контура сечения. Выполняя необходимые вычисления в табличной форме, получим ядро сечения.

Положение нейтральной линии	Отрезки, отсекаемые на осях		Координаты вершин ядра сечения
	ai	bi	xяi	yяi
1–1	∞	4t	0	–2,668t
2–2 (2'–2')	–4t (4t)	∞	1,083t (–1,083t)	0
3–3 (3'–3')	–4t (4t)	–16t	1,083t (–1,083t)	0,667t
4–4	∞	–8t	0	1,334t

4.2 Определение размеров сечения