Курсовая работа: Средства эконометрического моделирования и прогноза курса акций British Petroleum
Проверим, не образовал ли ряд третьих конечных разностей процесс случайного блуждания. Для этого проведём тест Дики – Фуллера.
Тест Дики–Фуллера
Таблица 4. Тест Дики–Фуллера для ряда третьих конечных разностей

Статистика Дики–Фуллера равна -13,27932. Все приведённые в таблице критические значения больше расчётного, максимальный уровень значимости, при котором можно отклонить гипотезу случайного блуждания – 0, поэтому гипотеза о наличии у процесса характера случайного блуждания отклоняется.
Закон распределения полученного ряда
Как видно из гистограммы, имеющей более вытянутую по вертикали форму, чем характерная для нормального распределения, и статистических показателей (рис. 5), распределение полученного ряда отлично от нормального: хотя коэффициент асимметрии равен 0,6, что близко к нулю и говорит о симметричности распределения относительно среднего значения, куртозис равен 11,918, что существенно больше трёх. Поскольку закон распределения не является нормальным, для проверки гипотезы о стационарности полученного ряда параметрические тесты неприменимы, и необходимо провести непараметрические тесты.
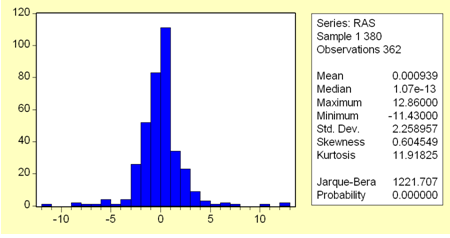
Рис. 5. Гистограмма распределения ряда третьих конечных разностей
Тест Вальда–Вольфовитца на постоянство математического ожидания
При проведении теста в ряду была обнаружена 271 серия, самая длинная из которых состоит из 4 элементов.
Согласно тесту, для того, чтобы математическое ожидание ряда было постоянным, длина самой длинной серии должна быть меньше ![]() ; и количество серий должно быть больше
; и количество серий должно быть больше
![]() .
.
Оба условия выполняются. Согласно тесту Вальда–Вольфовитца гипотеза о постоянстве математического ожидания ряда не может быть отклонена.
Тест Манна – Уитни на постоянство математического ожидания
T1 = 150 – количество элементов в первой части ряда;
T2 = 212 – количество элементов во второй части ряда;
R1 = 26982 – сумма рангов, присвоенных элементам из первой части ряда
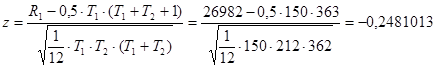 ,
, ![]()
В соответствии с тестом Манна–Уитни гипотеза о постоянстве математического ожидания не может быть отклонена.
Тест Сиджела–Тьюки на постоянство дисперсии
T1 = 150 – количество элементов в первой части ряда;
T2 = 212 – количество элементов во второй части ряда;
R1 = 26479 – сумма рангов, присвоенных элементам из первой части ряда
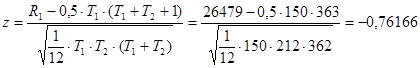 ,
, ![]()
Согласно тесту Сиджела–Тьюки гипотеза о постоянстве дисперсии не может быть отклонена.
Итак, полученный ряд можно рассматривать как стационарный.
Эконометрические модели для конечных разностей
Идентификация модели
Изучив вид автокорреляционной и частной автокорреляционной функций ряда (таблица 5), полученного с помощью конечных разностей, можно предположить, какая модель наилучшим образом будет описывать процесс.
Таблица 5. Коррелограмма ряда третьих конечных разностей
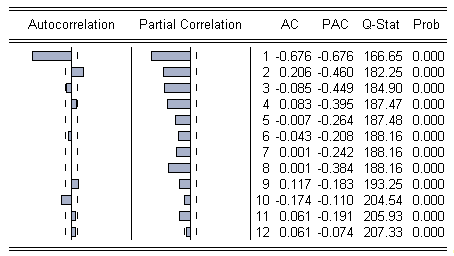
Первые два коэффициента автокорреляции ряда выходят за пределы доверительной трубки. Коэффициенты частной корреляции, вплоть до одиннадцатого включительно также выходят за пределы доверительной трубки, а их значения уменьшаются вплоть до шестого включительно.
Таблица 6. Критические значения для Q-Stat при уровне значимости 0,05
| t | 1 | 2 | 3 | 4 | 5 | 6 |
| Критическое значение | 3,84146 | 5,99146 | 7,81473 | 9,48773 | 11,0705 | 12,5916 |
| t | 7 | 8 | 9 | 10 | 11 | 12 |
| Критическое значение | 14,0671 | 15,5073 | 16,919 | 18,307 | 19,6751 | 21,0261 |
Критические значения, представленные в таблице 6, представляют собой квантиль хи квадрат распределения уровня значимости 0,05 со степенями свободы, равными количеству включаемых лагов («t» в таблице). Все значения Q-Stat (таблица 5) для ряда, полученного из исходного с помощью конечных разностей, превышают соответствующие критические значения (таблица 6). Это свидетельствует о наличии автокорреляции в полученном ряду, что позволит построить по нему модель, где в роли регрессоров выступают предыдущие значения ряда либо предыдущие значения ошибок модели.
Подобный вид автокорреляционной и частной автокорреляционной функций (таблица 5) характерен для моделей скользящего среднего второго порядка.