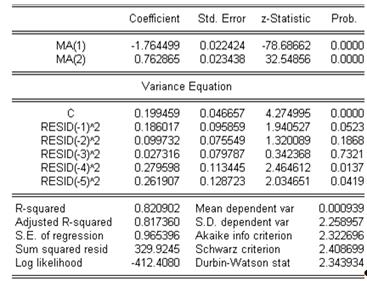
В соответствии с данной моделью процесс описывается уравнением:

А уравнение, характеризующее дисперсию ошибки, имеет вид:

Поскольку все коэффициенты в модели дисперсии ошибки положительны, дисперсия ошибки будет принимать только положительные значения, что соответствует смыслу показателя.

S.E. = 0,965396 < 2,258957 = S.D.

То есть модель снижает дисперсию процесса.

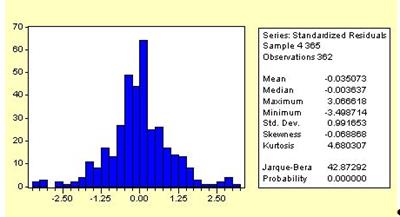
Рис. 6. Закон распределения ошибки модели MA(2)ARCH(5)

Гистограмма распределения ошибки (рис. 6) модели MA(2)ARCH(5) напоминает колокол нормального распределения, но, судя по статистическим показателям, распределение ошибки отлично от нормального: куртозис равен 4,68, что значительно превышает 3. Поэтому нельзя использовать параметрические тесты для определения статистической значимости регрессоров модели дисперсии ошибки.

Таблица 17. Автокорреляция ошибки модели MA(2)ARCH(5)

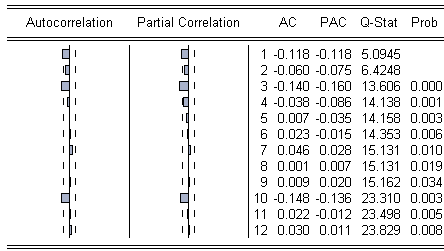
Первый, третий и десятый коэффициенты автокорреляции ошибки и частной корреляции ошибки выходят за пределы доверительной трубки. Уже первое значение Q-Stat (5,0945) превышает критическое (3,84146), что свидетельствует о невозможности принять гипотезу о равенстве нулю первого коэффициента автокорреляции ошибки модели. Таким образом, ошибка данной модели коррелированна.

Таблица 18. Автокорреляция квадратов ошибки модели MA(2)ARCH(5)

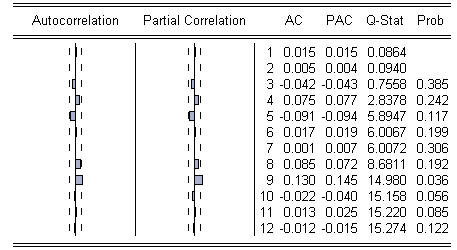
Двенадцатое расчётное значение Q-Stat равно 15,274, в то время как критическое значение составляет 21,0261. Поскольку расчётное значение меньше критического, нельзя отклонить гипотезу о равенстве нулю первых двенадцати коэффициентов автокорреляции квадратов ошибки. Таким образом, квадраты ошибки модели можно считать некоррелированными.

То есть данная модель избавила модель МА(2) от автокорреляции квадратов ошибок. Более того, значение критерия Акайке в данной модели составляет 2,322696, а значение критерия Шварца 2,408699, в то время как для МА(2) значения критериев соответственно равны 2,654312 и 2,675813.

Но при этом модель MA(2)ARCH(5) характеризуется автокоррелированной ошибкой, в то время как ошибка модели МА(2) представляет собой «белый шум».

Итак, более «ценным» для нас является отсутствие автокорреляции в ряду ошибки, чем отсутствие автокорреляции в ряду квадратов ошибки. Согласно тесту Сиджела–Тьюки дисперсия исследуемого ряда признана постоянной, а модель MA(2)ARCH(5) задаёт уравнение её изменения во времени. То есть, MA(2)ARCH(5) не может быть адекватна процессу, и лучшей из рассмотренных моделей признаётся МА(2).

Соответствие модели МА(2) данным

В таблице 19 представлены данные, рассчитанные по модели МА(2), на последние десять временных периодов и фактические значения ряда конечных разностей.

Таблица 19. Рассчитанные по модели МА(2) и фактические значения ряда конечных разностей

Дата	МА(2)	Конечные разности
22.12.2010	0,351424	0,35
23.12.2010	-0,207641	0,11
24.12.2010	-0,623400	-0,7175
25.12.2010	0,473950	0,3975
26.12.2010	0,081419	0
27.12.2010	0,079003	0
28.12.2010	0,135444	0,1475
29.12.2010	-0,230865	-0,4475
30.12.2010	0,530154	0,4
31.12.2010	0,025743	0,24

Полученные по модели значения в конце периода близки к фактическим значениям конечных разностей. Для оценки адекватности данным более наглядным будет использование графика.

Как видно на графике (рис. 7), значения, полученные по модели, близки к фактическим значениям конечных разностей третьего порядка, но «опаздывают» на один шаг – особенно заметны отличия в середине ряда, где фактические значения сильнее отклоняются от своего среднего значения. Это связано с тем, что модель скользящего среднего строится по ошибкам прошлых периодов, поэтому в случае резкого скачка в исходных данных модель не сможет его предугадать, и в следующем периоде будет получено значение, близкое к «скачку». Следует отметить, что в конце периода фактические значения не сильно отклоняются от своего среднего, и данные, рассчитанные по модели, близки к фактическим. Это позволяет рассчитывать на адекватный прогноз по модели.

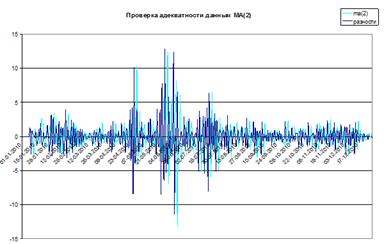
Рис. 7. Конечные разности третьего порядка и модель МА(2)

Прогноз по МА(2)

Прогноз по модели МА(2) считается как , где i – номер прогнозируемого периода. Поскольку модель скользящего среднего строится по ошибкам, прогноз можно построить на ограниченный период времени: будущие ошибки неизвестны и не могут быть использованы в расчётах. В частности, для модели МА(2) прогноз может быть построен на два периода. Результаты представлены в таблице 20.

Таблица 20. Прогнозные значения конечных разностей

Дата	Прогноз
01.01.2011	-0,544291
02.01.2011	0,205299

Возврат к исходному ряду