Курсовая работа: Статистический пакет STATISTIKA
4) Проверить значимость построенной модели (например, используя уровень значимости α=0,05 ).
5) Если модель значима дать оценку коэффициентов множественной регрессии на основе t -критерия, если tтабл (15-4-1)= tтабл (10)=2,2281 и уровня значимости α=0,05 .
6) Пересчитать уравнение множественной регрессии используя только значимые факторы.
7) Проверить адекватность регрессионной модели (полученной на предыдущем этапе анализа).
8) Осуществить прогнозирование в соответствии с вариантом
9) Оформить отчет о проделанной работе используя распечатки отчета, полученного средствами пакета STATISTICA или в MS Word.
Порядок выполнения задания
В системе STATISTICA для построения корреляционной матрицы можно воспользоваться модулем Basic Statistics/Tables (Основные статистики и таблицы), выбрав процедуры 
®
, используя в качестве переменных все исходные данные (Select all). И процедуру 
для представления матрицы в графическом виде.
По корреляционной матрице можно в первом приближении судить о тесноте связи факторных признаков х1 , х2 ,…,xm между собой и с результативным признаком y , а также осуществлять предварительный отбор факторов для включения их в уравнение регрессии. При этом не следует включать в модель факторы, слабо коррелирующие с результативным признаком и тесно связанные между собой. Не допускается включать в модель функционально связанные между собой факторные признаки, так как это приводит к неопределенности решения.
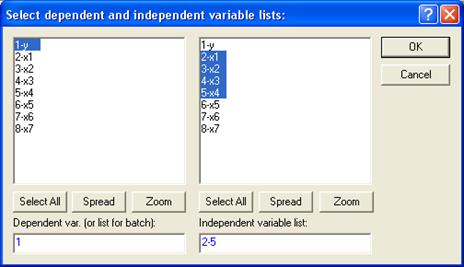
Выбор уравнения модели, в большинстве случаев, производятся среди функций перечисленных в таблице 3. В системе STATISTICA для построения линейного уравнения множественной регрессии можно воспользоваться модулем множественной регрессии 
, определив зависимую (dependent) переменную y и независимые (independent) переменные х1 , х2 , x3 , x4 .
Статистический вывод о пригодности (значимости) уравнения регрессии в системе Statistica обычно проверяется в следующей последовательности.
10.Проводится общаяпроверка модели, целью которой является выяснение, объясняют ли х -переменные значимую долю изменения у . Определение значимости модели рекомендуется проводить по следующим методам (см. табл. 5).
Таблица 5
| Критерий Фишера | Использование уровня значимости α | Использование коэффициента детерминации R2 |
| Проверяется нулевая гипотеза H0 о равенстве полученных коэффициентов регрессии нулю: a0 =a1 =a2 =…=am =0 . Для этого рассчитанное системой Statistica значение F -критерия (Fрасч ), сравнивается с табличным значением Fтабл , определяемым с использованием специальных таблиц по заданным уровню значимости (например, a =0,05 ) и числу степеней свободы (df1=m, df2=n-m-1 ). Если выполняется неравенство Fрасч < Fтабл , то с уверенностью, например на 95 %, можно утверждать, что рассматриваемая зависимость y = а0 + a1 x1 + … +am xm является статистически значимой. |
Если рассчитанное в Statistica значение уровня значимости р больше, чем заданный уровень значимости a (например, a =0,05) , то полученный результат нужно трактовать как незначимый (для 95% вероятности). В том случае, когда величина р <0,05, то вывод такой: это значимое уравнение с вероятностью 95%. | Рассчитанная системой Statistica величина  сравнивается с табличными (критическими) значениями  , определяемым с использованием специальных таблиц по заданному уровню значимости (например, α =0,05 ). Если окажется, что >, то с упомянутой степенью вероятности (95 %) можно утверждать, что анализируемая регрессия является значимой. |
Если регрессия неявляется значимой, то говорить больше не о чем.
В при веденном примере модель значима, т.к. вычисленный уровень значимости модели р =0,000000<0,05.
Осуществив переход к результатам регрессии (Summary: Regression results) получаем уравнение линейной множественной регрессии вида y(x1 , x2 , x3 , x4 )=6,9+0,07x1 –0,00035x2 –2,08x3 +0,00003x4 :
 |
2. Если регрессия оказывается значимой, то существует взаимосвязь между параметром у и переменными х1 , х2 ,…,xm . Однако остается неясно, каково влияние конкретных факторов х1 , х2 ,…,xm на исследуемую функцию у . Можно продолжить анализ, используя t- тесты для отдельныхкоэффициентов регрессии а0 , a1 ,a2 ,…,am с целью выяснить, насколько значимой является влияние той или иной переменной х на параметр у при условии, что все другие факторы хk остаются неизменными. Проверку на адекватность коэффициентов регрессии рекомендуется проводить по следующим эквивалентным методам (см. табл. 5).
Таблица 5
| Использование t-критерия Стьюдента | Использование уровня значимости α |
| Анализируемый коэффициент а0 , a1 ,a2 ,…,am считается значимым, если рассчитанное системой Statistica для него значение t -критерия по абсолютной величине превышает tтабл , определяемым с использованием специальных таблиц по заданным уровню значимости (например, a =0,05 ) и числу степеней свободы (df=n-m-1 ). | Коэффициент регрессии а0 , a1 ,a2 ,…,am признается значимым, если рассчитанное системой Statistica для него значение уровня значимости р меньше (или равно) 0,05 (для 95%-ной доверительной вероятности). |
Т.к. вычисленные уровни значимости p-level для коэффициентов, стоящих при x2 и x4 меньше 0,05, то они не значимы. К аналогичному выводу можно прийти, воспользовавшись t -критерием: t2 (10)=-0,013<2,228 и t3 (10)=1,44<2,228.
С учетом этого факта, пересчитаем уравнение множественной регрессии, выбрав в качестве зависимой (dependent ) переменную y и независимые (independent ) переменные х1 и x3 , коэффициенты при которых значимы:
Получаем:
