Курсовая работа: Статистично-економічний аналіз і прогнозування ефективності виробництва озимої пшениці за матеріалами

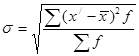(1.6)

Середній квадрат відхилень – дисперсія:

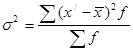, (1.7)

де - середнє арифметичне інтервального ряду розподілу, f – частота.

Середнє лінійне та середнє квадратичне відхилення – іменовані числа (в одиницях вимірювання ознаки).

Порівнюючи варіації різних ознак або однієї ознаки у різних сукупностях, використовують відносні характеристики варіації. Коефіцієнти варіації розраховуються як відношення абсолютних, іменованих характеристик до центру розподілу і часто виражаються процентами:

Лінійний коефіцієнт варіації:

(1.8)

Квадратичний коефіцієнт варіації:

(1.9)

1.3 Динамічні ряди та їх характеристики

Динамічний ряд – це розміщені у хронологічній послідовності значення певного статистичного показника. складовими динамічного ряду є ознака часу (момент або інтервал) та числові значення показника – рівні.

Визначають абсолютні та відносні характеристики динаміки: абсолютний приріст та абсолютне значення 1% приросту; темп зростання та темп приросту. Розрахунок їх грунтується на порівнянні рівнів динамічного ряду. Якщо база порівняння постійна, характеристики динаміки називаються базисними, якщо база порівняння змінна – ланцюговими.

Абсолютний приріст (зменшення) – це різниця рівнів динамічного ряду:

базисні

(1.10)

ланцюгові

(1.11)

Сума ланцюгових абсолютних приростів дорівнює кінцевому базисному приросту

Темп зростання розраховується як відношення рівнів ряду, виражається коефіцієнтом або процентом:

базисні

(1.12)

ланцюгові

(1.13)

Добуток ланцюгових темпів зростання дорівнює кінцевому базисному.

Темп приросту показує, на скільки процентів рівень більше рівня, взятого за базу порівняння. Його можна визначити як відношення абсолютного приросту до бази порівняння або безпосередньо на основі темпу зростання.

(1.14)або (1.15)

Абсолютне значення 1% приросту показує, чого вартий 1%; розраховується як співвідношення абсолютного приросту і темпу приросту:

(1.16)