Курсовая работа: Структуризация задач принятия решений в условиях определенности Некорректно поставленные задачи

Хорошо известным примером некорректно поставленной задачи является интегральное уравнение Фредгольма 1-го рода. Пусть оператор A имеет вид:

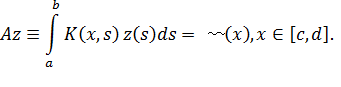
Пусть ядро интегрального оператора K (x , s ) - функция, непрерывная по совокупности аргументов x ∈[c , d ], s ∈[a ,b ], а решение z (s ) - непрерывная на отрезке [a ,b ] функция. Тем самым, можно рассматривать оператор A как действующий в следующих пространствах: A :C [a ,b ]→ C [c , d ]. (Пространство C [a ,b ] состоит из функций, непрерывных на отрезке [a ,b ]. Норма z ∈C [a ,b ]определяется как ). Покажем, что в этом случае задача решения интегрального уравнения является некорректно поставленной. Для этого нужно проверить условия корректности постановки задачи:

1) Существование решения для любой непрерывной на [c , d ] функцииu (x ) . На самом же деле, это не так: существует бесконечно много непрерывных функций, для которых решения нет.

2) Единственность решения. Это условие выполняется в том и только в том случае, если ядро интегрального оператора замкнуто.

Первые два условия корректности эквивалентны условию существования обратного оператора с областью определения D( )=C [c ,d ]. Если ядро интегрального оператора замкнуто, то обратный оператор существует, однако область его определения не совпадает с C [c ,d ].

3) Устойчивость решения. Это означает, что для любой последовательности последовательность z n →. Устойчивость эквивалентна непрерывностиобратного оператора при условии, что обратный оператор существует. В данном случае это нетак, что видно из следующего примера. Пусть последовательность непрерывных функций , n= 1, 2, … , такая, что на промежутке и обращается в нуль вне данного интервала, max| z (s ) |=1, s ∈[a , b ], а последовательность чисел d → 0 +0 .

4) Такая функция может быть выбрана, например, кусочно-линейной. Тогда для любого x ∈[c , d ]

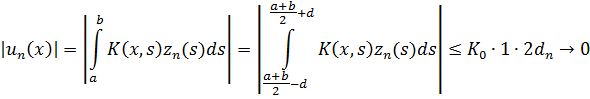
при

Последовательность функций равномерно, т.е. по норме C [c ,d ], сходится к = 0.

Хотя решение уравнения в этом случае = 0 , последовательность не стремится к , так как.

Интегральный оператор A является вполне непрерывным при действии из в

, при действии из C [a ,b ] в и при действии из C [a ,b ] в C [c ,d ]. (Пространство

состоит из функций, интегрируемых с квадратом на отрезке [a ,b ]. Норма z ∈определяется как ). Это означает, что любую ограниченнуюпоследовательность этот оператор преобразует в компактную. Компактная последовательность поопределению обладает тем свойством, что из любой ее подпоследовательности можно выделитьсходящуюся. Легко указать последовательность , , из которой нельзя выделить сходящуюся в C [a ,b ] подпоследовательность. Например,

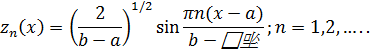
Нормы всех членов этой последовательности равны 1 в , но из любой подпоследовательности этой последовательности нельзя выделить сходящуюся, поскольку . Очевидно, что эта последовательность состоит из непрерывных на [a ,b ] функций и равномерно (по норме C [a ,b ]) ограничена, но из этой последовательности нельзя выделить сходящуюся в C [a ,b ] подпоследовательность (тогда она сходилась бы и в , поскольку из равномерной сходимости следует сходимость в среднем). Если предположить, что оператор является непрерывным, то легко прийти к противоречию. Для существования обратного оператора достаточно потребовать, чтобы прямой оператор A был инъективным. Очевидно, что, если оператор B : C [c ,d ]→C [a ,b ] непрерывный, а оператор A вполне непрерывный, то BA :C [a ,b ] →C [a ,b ] - тоже вполне непрерывный оператор. Но тогда, поскольку для любого n , то последовательность компактна, что неверно. Оператор, обратный к вполне непрерывному оператору, не может быть непрерывным. Аналогичное доказательство может быть проведено для любых бесконечномерных банаховых (т.е. полных нормированных) пространств.

Поскольку задача решения интегрального уравнения Фредгольма первого рода в указанных пространствах некорректно поставлена, то даже при очень малых ошибках в задании u (x ) решение может либо отсутствовать, либо как угодно сильно отличаться от искомого точного решения.

Итак, вполне непрерывный инъективный оператор обладает обратным оператором, который не является непрерывным (ограниченным). Более того, при действии в бесконечномерных банаховых пространствах множество значений вполне непрерывного оператора не является замкнутым. Поэтому как угодно близко к неоднородности u (x ) , для которой решение операторного уравнения существует, найдется неоднородность, для которой решение отсутствует.

Некорректность постановки математической задачи может быть связана с ошибкой в задании оператора. Простейший пример дает задача отыскания нормального псевдорешения системы линейных алгебраических уравнений и возникающая при этом неустойчивость, связанная с ошибками задания матрицы.

Пусть дана система линейных алгебраических уравнений (СЛАУ):

Система может и не иметь решений. Гаусс и Лежандр в начале XIX века ввели метод наименьших квадратов, а именно, вместо решения СЛАУ предложили минимизировать квадратичный функционал (невязку):

- сопряженная (транспонированная) матрица. Поскольку матрица неотрицательно

определена, то Ф (x )- выпуклый функционал. Для выпуклого функционала задача отыскания эквивалентна отысканию стационарной точки, т.е. решения уравнения Ф '(x ) = 0 . Легко видеть, что Ф ' (x ) = 2 ⋅(Ax −b ), Ф ''(x ) = 2 ⋅A ≥0.

Из равенства градиента нулю получается система линейных алгебраических уравнений с квадратной неотрицательно определенной матрицей (система нормальных уравнений):

В конечномерном случае легко доказать, что для любого вектора b система нормальных