Курсовая работа: Суперэлементное моделирование пространственной системы "плита – грунтовое основание"
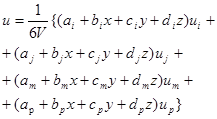(4), где
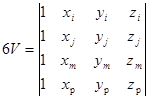(5а)
Величина V в данном случае представляет собой объем тетраэдра. Коэффициентами 
обозначены определители
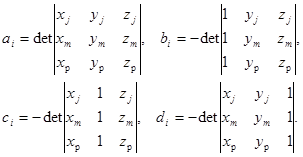(5б)
Остальные коэффициенты получаются циклической перестановкой индексов i, j, p, m.
Как видно из фигуры 1, узлы i, j, p, m пронумерованы в соответствии с правилом правой руки, причем первые три узла пронумерованы по часовой стрелке, если смотреть со стороны последнего узла.
Перемещение элемента определяется двенадцатью компонентами перемещений его узлов:
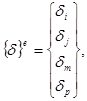(6) где
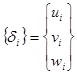и т.д.
Перемещение произвольной точки можно записать в виде
(7)
где скалярные величины определяются соотношениями
и т.д.
А I- единичная матрица размерности 3*3.
Ясно, что эти функции перемещений будут удовлетворять требованиям непрерывности на границах между элементами. Этот результат является прямым следствием линейного закона изменения перемещений.
4.2 Матрица деформации
В трехмерном случае учитываются все шесть компонент деформации. Используя известные обозначения Тимошенко, запишем матрицу деформаций в виде
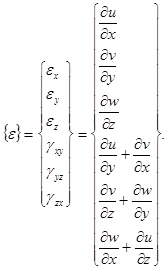(9)
С помощью соотношений (4) - (7) легко убедиться, что
(10) где
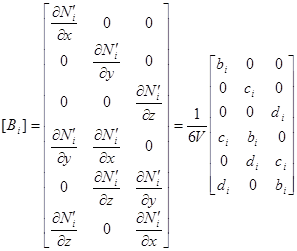. (11)
Остальные подматрицы получаются простой перестановкой индексов.
Начальные деформации, такие, как обусловленные тепловым расширением, можно записать обычным образом в виде шестикомпонентного вектора, имеющего, например, для изотропного теплового расширения простой вид:
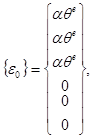(12)
где
- коэффициент линейного расширения, а 
- средняя по элементу температура.
4.3 Матрица упругости
В случае материала с изотропией свойств матрица [D], связывающая шесть компонент напряжения с компонентами деформации, может содержать не более чем 21 независимую постоянную.
В общем случае
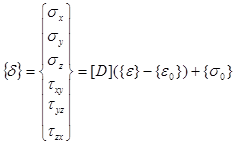. (13)
Так как такое умножение никогда не выполняется в явном виде, запишем здесь матрицу [D] только для изотропного материала, хотя это нетрудно сделать и для случая произвольной анизотропии. При использовании обычных упругих постоянных: модуля упругости Е и коэффициента Пуассона v- матрица имеет вид
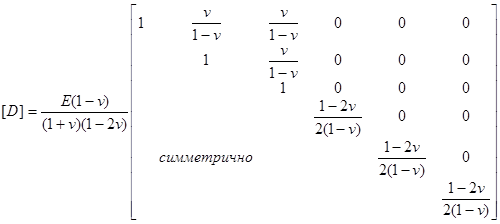(14)