Курсовая работа: Суперэлементное моделирование пространственной системы "плита – грунтовое основание"
Подматрица с индексами rs матрицы жесткости имеет размерность 3*3 и определяется соотношением
![]() , (15)
, (15)
где V- объем тетраэдра.
Узловые силы, обусловленные начальной деформацией, записываются в виде
![]() , (16) или для i-ой компоненты
, (16) или для i-ой компоненты
![]() .
.
5. Математическая и дискретная модели
5.1 Математическая модель
Математическая модель системы включает геометрическую, структурную, механико-математическую модели, краевые условия и условия равновесия системы.
Геометрическая модель представляет собой параллелепипед, размеры которого определяются нулевыми перемещениями на его ребрах.
Механико-математическая модель системы “плита-основание”: для основания si =E i ei , для плиты si =E’ ei , E’>>Ei , где E’, Ei -модули упругости основания и плиты, si, ei -интенсивности напряжений и деформаций.
Краевые условия области определения системы “плита-основание": перемещения на всех ребрах, кроме верхнего равны нулю, на верхнем ребре области определения на поверхности плиты задается внешняя нагрузка.
5.2 Дискретная модель
Процесс дискретизации разделяется на 2 этапа:
Разбиение области на подобласти. Подобласти характеризуются стационарностью определяющих характеристик: свойства материала, прилагаемая нагрузка.
Разбиение подобластей на конечные элементы. Подобласти разбиваются на симплекс-элементы.
Дискретизация производится элементами малых размеров. Деформация и напряжение в любом конечном элементе выражаются через перемещения по известным формулам. В узлах элементов вводятся силы, статистически эквивалентные напряжениям на границе соответствующего элемента и внешним силам, приложенным к нему.
Разбивка на элементы производится так, что в пределах одного элемента участок среды рассматривается как однородный. Любой другой элемент, оставаясь однородным, может характеризоваться свойствами, отличными от соседних элементов. Таким образом, система в целом представляет неоднородную среду.
Применение МКЭ для решения системы “плита-основание” приводит к системе линейных алгебраических уравнений с ленточной симметричной матрицей. Ширина ее полуленты зависит от порядка нумерации узлов и определяется по формуле: B= (R+1) Q, где R - максимальная разность разностей номеров узлов конечных элементов, Q - число неизвестных (степеней свободы) в каждом узле.
6. Алгоритмы построения и решения дискретной модели
Первый этап алгоритма построения дискретной модели представляет определение расчетной области. Расчетная область представляется правильной геометрической фигурой, размеры которой определяются нулевыми перемещениями на всех ребрах, кроме верхнего. В нашем случае- параллелепипед.
Второй этап- дискретизация расчетной области, учитывающая особенности структуры грунтового основания. В результате строится нерегулярная решетка с массивами шагов по координатным осям. Каждый параллелепипед дискретной решетки делится на шесть тетраэдральных элементов.
Для каждого конечного элемента (тетраэдра) необходимо задать характеристики: модуль упругости, коэффициент Пуассона.
Третий этап - задание краевых условий. Граничные условия расчетной области определяются системой внешних сил и выбором размеров расчетной области (этап 1). Система внешних сил задается в виде вектора нагрузок, определенного для всех узлов расчетной области. С каждым узлом связано три значения нагрузки: одно по направлению оси OX, второе по направлению оси OY, третье по направлению оси OZ. Вектор нагрузок задается на верхнем ребре. На всех остальных обычно задаются нулевые перемещения. Четвертый этап - формирование матрицы жесткости. Построение матрицы жесткости производится с учетом ее особенностей: симметричности, ленточности. Матрица жесткости (МЖ) размещается в ОП упакованной в прямоугольник, т.е. хранится верхняя полулента. Для построения МЖ используется аналитический алгоритм построения [1].
Согласно которому матрица жесткости имеет вид:
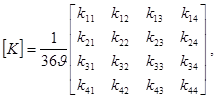 где
где
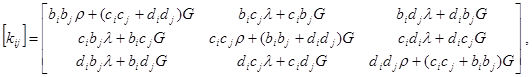
где i - номер узла, связанного с узлами j; j=1,2,3,4 ; ![]()
Пятый этап - учет граничных условий в МЖ. Используется вектор усилий и вектор корректировки, с помощью которого описываются задаваемые граничные значения перемещений. Учёт граничных условий приводит к изменению матрицы жёсткости [K ] и векторов узловых сил и перемещений. Матрица [K ] уже не будет сингулярной.
Шестой этап - решение системы линейных алгебраических уравнений. На этом этапе используется метод квадратного корня, учитывающий упаковку МЖ в прямоугольник.
Этот метод состоит в следующем:
Если матрица симметрическая, то её можно представить следующим образом:
A=S*DS,