Курсовая работа: Суперэлементное моделирование пространственной системы "плита – грунтовое основание"
i=j то, ![]() ;
;
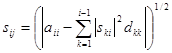 ;
;
i<j то
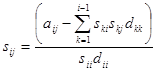 ;
;
В том случае, если матрица A самосопряжённая и положительно определённая, то матрицу D можно опустить, так как она будет единичной. Метод осуществляется по следующей схеме:
сначала решаем уравнение S*Y=B
затем уравнение SX=Y, находя решение системы.
Наша работа заключается в решении СЛАУ методом квадратного корня, используя ленточную симметрическую матрицу, компактно упакованную.
Полуленточная матрица системы строиться следующим образом:
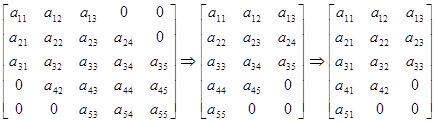
В методе квадратного корня используется функция, с помощью которой меняются оба индекса.
7. Описание и инструкция работы с приложением
Входными данными для приложения являются: количество узлов по осям, массивы узлов, модуль упругости и коэффициент Пуассона для каждого симплекс-элемента, а также вектора узловых сил и пермещений.
Пользователю имеет возможность задавать характеристики каждого отдельного симплекс-элемента (тетраэдра). Благодаря этому система “плита-грунтовое основание" может быть рассмотрена как неоднородная.
Ввод вектора узловых сил осущестляется путем ввода величины силы узлу к которому она прилагается. Вектор перемещений сразу предполагает перемещения по трем осям. Однако пользователь имеет возможность запретить перемещения по какой-либо оси для каждого узла.
Выходными характеристиками приложения являются перемещениями в необходимых узлах. По анализу которых делается вывод об осадке плиты.
8. Верификация приложения
Рассмотрим следующий пример:
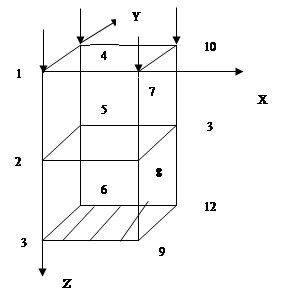 |
Однородная плита располагается вертикально на жёстком основание. Усилие Р равномерно распределено по верхнему основанию плиты. Дискретизация пластины производится путём разбиения ее на конечные элементы (тетраэдры). Узлы и полученные конечные элементы нумеруются. Программное приложение рассчитывает значения перемещений в каждом узле модели.
При введении в качестве параметров модели тестового примера следующих величин: нагрузка на плиту Р = 100кг,
параметры плиты: модуль упругости Е = 360 кг/см2 , коэффициент Пуассона m=0.2, h=100см, l =100см, приращения по Ox,Oy, Oz =50см.
Разрешены только вертикальные перемещения.
Полученный результат имеет вид:
вертикальные перемещения в узлах:
1.09651.03951.06241.0996
0.53560.53080.53420.5345
0.00000.00000.00000.0000
Заключение
В курсовой работе реализовано моделирование расчета осадок большеразмерной плиты на основании системного подхода и метода конечных элементов. Разработаны алгоритмы построения матрицы жесткости упакованной в прямоугольник, решения системы линейных алгебраических уравнений для упакованной МЖ. Спроектирован удобный интерфейс ввода исходных данных и вывода результатов. Создан программный продукт моделирования расчета осадок в среде Delphi 5.0.
Проведена верификация программного продукта на основе задачи, имеющей аналитическое решение. Она показала хорошее совпадение результатов с точностью примерно 90-95%.
Разработанное приложение может быть использовано для предварительных расчетов оснований фундаментов плит с учетом сложной структуры основания в инженерной практике на этапе проектирования.
Список использованных источников
1. Быховцев В.Е. Компактный алгоритм построения матрицы жесткости в МКЭ. - Известия АН БССР, серия физ. - матем. наук, №1, 1983, с.34-37.