Курсовая работа: Течение Пуазейля
т. е. уравнение (2) будет иметь вид
![]()
или
![]() (3)
(3)
гдеdс/dt— полная производная плотности.
Для установившегося движения сжимаемой жидкости∂с/∂t = 0 и. следовательно, из уравнения (2) получаем
![]() (4)
(4)
Для любого движения несжимаемой жидкости с = const и, следовательно
![]() (5)
(5)
3. Уравнение движения вязкой жидкости в форме Навье-Стокса
Уравнение движения жидкости в напряжениях:
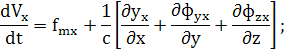
![]() (6)
(6)
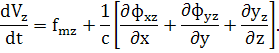
Согласно закону Ньютона вязкостные напряжения при прямолинейном движении жидкости пропорциональны скоростям угловых деформаций. Обобщением этого факта на случай произвольного движения является гипотеза о том, что касательные напряжения, а также зависящие от ориентации площадок части нормальных напряжений пропорциональны соответствующим скоростям деформаций. Иными словами, предполагается во всех случаях движения жидкости линейная связь между вязкостными напряжениями и скоростями деформаций. При этом коэффициент пропорциональности в формулах, выражающих эту связь, должен быть динамический коэффициент вязкости м. Воспользовавшись гипотезой, что в точке жидкости ![]() (она косвенно подтверждается на практике), можно написать выражения для нормальных и касательных напряжений в вязкой жидкости:
(она косвенно подтверждается на практике), можно написать выражения для нормальных и касательных напряжений в вязкой жидкости:
![]()
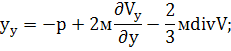
![]()
![]() (7)
(7)
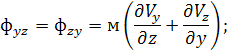
![]()
Внося в уравнение (6) выражения (7), получим



Группируя члены со вторыми производными, деля на с и используя оператор Лапласа, запишем:
![]()
![]() (8)
(8)
![]()
Эти уравнения называются уравнениями Навье — Стокса; их используют для описания движений вязких сжимаемых жидкостей и газов.