Курсовая работа: Технологии цифровой связи

Рассмотрим особенности обоих видов угловой модуляции: фазовой и частотной.

Фазовая модуляция заключается в пропорциональном первичному сигналу x(t) изменении фазы φ переносчика

. (9)

где а — коэффициент пропорциональности. Амплитуда колебания при фазовой модуляции не изменяется, поэтому аналитическое выражение ФМ колебания

. (10)

Если модуляция осуществляется гармоническим сигналом x(t) =Xsin Ωt, то мгновенная фаза

. (11)

Первые два слагаемых (10) определяют фазу немодулированного колебания, третье — изменение фазы колебания в результате модуляции.

Фазомодулированное колебание наглядно характеризуется векторной диаграммой рисунок 4, построенной на плоскости, вращающейся по часовой стрелке с угловой частотой w₀ . Немодулированному колебанию соответствует неподвижный вектор U₀ . Фазовая модуляция заключается в периодическом с частотой Ω повороте вектора U относительно U₀ на угол ∆φ(t)=aXsinΩt. Крайние положения вектора U обозначены U’ и U’’. Максимальное откло­нение фазы модулированного колебания от фазы немодулированного колебания

M=∆φ_max =aX. (12)

называется индексом модуляции. Индекс модуляции М пропорционален амплитуде Х модулирующего сигнала. Он в такой же степени характеризует ФМ колебание, как коэффициент модуляции т — AM колебание.

Рисунок 4 - Векторная диаграмма фазомодулированного колебания

Используя (11), перепишем ФМ колебание (9) как

. (13)

Мгновенная частота ФМ колебания

. (14)

Таким образом, ФМ колебание в разные моменты времени имеет различные мгновенные частоты, отличающиеся от частоты несущего колебания на величину , что позволяет рассматривать ФМ колебание как модулированное по частоте.

Наибольшее отклонение частоты ω от ω₀ называется девиацией частоты ∆ω_Д . Согласно (13):

∆ω_д =MΩ или ∆f_Д =MF. (15)

Частотная модуляция заключается в пропорциональном первичному сигналу x(t) изменении мгновенной частоты переносчика:

ω=ω₀ +ax(t). (16)

где а — коэффициент пропорциональности. Мгновенная фаза ЧМ колебания: .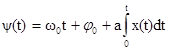

Аналитическое выражение ЧМ колебания с учетом постоянства амплитуды можно записать в виде:

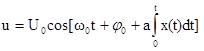. (17)

В простейшем случае модуляции гармоническим колебанием мгновенная частота , где — девиация частоты, т. е. максимальное ее отклонение от несущей частоты ω₀ , вызванное модуляцией. Аналитическое выражение этого ЧМ колебания: .

Слагаемое характеризует изменение фазы, получающееся при ЧМ. Это позволяет рассматривать ЧМ колебание, как ФМ колебание с индексом модуляции

, (18)

и записать его аналогично: