Курсовая работа: Технология работы шагового двигателя
Анализируя полученные результаты моделирования, можно сделать вывод о том, что переходя от нелинейности, которая описывается полиномом 3го порядка, к кусочно-непрерывным линейным функциям, качество системы практически не изменяется.
2. Шаговый двигатель
2.1 Описание шагового двигателя
Штатный регулятор совмещает в себе регулирующее устройство и исполняющий элемент. В качестве альтернативы предлагается использовать сервопривод, управляемый шаговым двигателем. Необходимость сервопривода обусловлена тем, что мощности шагового двигателя недостаточно для перемещения рейки, отвечающей за подачу топлива. Поэтому шаговый двигатель будет выполнять функции регулирующего устройства, а сервопривод – исполняющего. В связи с этим, структурная схема САР примет вид:
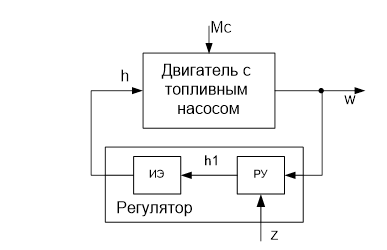
Рис.18. Модифицированная структурная схема САР двигателя.
Таблица 5 «Величина хода штока электродвигателя»
| Положение штока | Число шагов электродвигателя | Величина хода штока электродвигателя, мм |
| 1- «минимальный вылет» | 0 | 0,0 |
| 2- «рабочий ход» | 264 | 11,000±0,066 |
| 3- «максимальный вылет» | 312 | 13,00 ±0,08 |
| Примечание - Величина хода штока при выдвижении и втягивании на 1 мм соответствует 24 шагам электродвигателя | ||
Параметры импульсов управления
Временные диаграммы импульсов управления электродвигателем (скорость вращения ротора двигателя 168 шаг/с - скорость перемещения штока 7 мм/с).
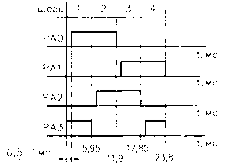
Рис.20. Втягивание штока.
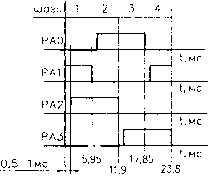
Рис.21. Выдвижение штока.
2.2 Разработка схемы управления двигателем
2.2.1 Получение последовательности выходных импульсов
Для того чтобы реализовать управляющие импульсы, воспользуемся подходом построения счетчика с произвольным порядком счета.
Необходимость в таких устройствах возникает при проектировании автоматов для выдачи отдельных сигналов включения и выключения устройств в определенной последовательности.
Рассмотрим построение такого счётчика на JK-триггерах. Получим последовательность выходных состояний счётчика. Для этого определим величину одного кванта времени D как наибольший общий делитель (НОД) из длительностей импульсов 
и интервалов между ними 
для всех выходов (рис.20-21).
Результатом является квант времени D, равный 0.35mc.
Выходная последовательность будет иметь вид РА0, РА1, РА2, РА3.
Необходимо доопределить 4-разрядные коды (РА0, РА1, РА2, РА3) до n -разрядных таким образом, чтобы среди них не было одинаковых.
n по формуле:
,
где 
– знак округления до ближайшего справа целого числа.
m – количество выходов;
к – максимальное число одинаковых кодов.
В нашем случае, m=4, k=15, n=8.
Чтобы исключить одновременного изменения состояния двух разрядов, будем доопределять последовательность кодами Грея. Код Грея относится к таким, в которых при переходе от любой кодовой комбинации к следующей изменяется только один разряд. В схемотехнике счетчиков это свойство устраняет одновременное переключение многих разрядов, характерное для двоичных счетчиков при некоторых переходах. Одновременное переключение многих элементов создает такие токовые импульсы в цепях питания схем, которые могут вызывать сбои в работе схемы.
В результате получим последовательность, представленную в Приложении 1.
Последовательность имеет 68 устойчивых неповторяющихся состояний. Для построения такого счётчика необходимо 8 триггеров. Выберем JK – триггеры.
2.2.2 JK – триггер
Триггеры – элементарные автоматы, содержащие собственно элемент памяти (фиксатор) и схему управления. Фиксатор строится на двух инверторах, связанных друг с другом «накрест», так что выход одного соединен с входом другого. Такое соединение дает цепь с двумя устойчивыми состояниями (рис. 22). Действительно, если на выходе инвертора 1 имеется логический нуль, то он обеспечивает на выходе инвертора 2 логическую единицу, благодаря которой сам и существует. То же согласование сигналов имеет место и для второго состояния, когда инвертор 1 находится в единице, а инвертор 2 – в нуле. Любое из двух состояний может существовать неограниченно долго.
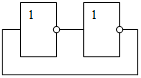
Рис. 22. Ячейка с двумя устойчивыми состояниями.