Курсовая работа: Технология работы шагового двигателя
Рис. 23. Схемы фиксаторов с входами управления на элементах ИЛИ-НЕ и И-НЕ
Переходное состояние, в котором инверторы активны, неустойчиво. Это можно показать, имея в виду, что напряжения в любой цепи не являются идеально постоянными, а всегда имеют место флуктуации. Флуктуации обязательно приведут фиксатор в одно из двух стабильных состояний, т. к. из-за наличия в схеме петли положительной обратной связи любое изменение режима вызывает продолжение в том же направлении, пока фиксатор не перейдет в устойчивое состояние, когда петля обратной связи как бы разрывается вследствие потери инверторами усилительных свойств (переход в режимы отсечки и насыщения, свойственные устойчивым состояниям).
Чтобы управлять фиксатором, нужно иметь в логических элементах дополнительные входы, превращающие инверторы в элементы И-НЕ либо ИЛИ-НЕ. На входы управления поступают внешние установочные сигналы.
Установочные сигналы показаны на рис. 23 штриховыми линиями. Буквой R латинского алфавита (от Reset) обозначен сигнал установки триггера в нуль (сигнал сброса), а буквой S (от Set) – сигнал установки в состояние логической единицы (сигнал установки). Состояние триггера считывается по значению прямого выхода, обозначаемого как
. Чаще всего триггер имеет и второй выход с инверсным сигналом 
. Для фиксатора на элементах ИЛИ-НЕ установочным сигналом является единичный, поскольку только он приводит логический элемент в нулевое состояние независимо от сигналов на других входах элемента. Для фиксатора на элементах И-НЕ установочным сигналом является нулевой, как обладающий тем же свойством однозначно задавать состояние элемента независимо от состояний других входов.
Таблицу истинности триггера JK можно записать в полном (табл. 6) или сокращенном виде (табл. 7). Через 
обозначено новое состояние триггера (после переключения).
Таблица 6
 |  | | | Режим |
| 0 | 0 | 0 | 0 | Хранение |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | Установка 0 |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | Установка 1 |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | Переключение |
| 1 | 1 | 1 | 0 |
Таблица 7
| | |
| 0 | 0 | Q |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 |  |
Карта Карно для JK-триггера показана на рис. 24. Из неё можно получить характеристическое уравнение триггера 
.
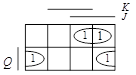
Рис. 24. Карта Карно для JK-триггера
По характеристическому уравнению можно построить схему триггера в любом логическом базисе (рис. 25).
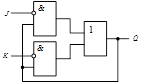
Рис. 25. Схема JK-триггера в базисе И, ИЛИ, НЕ
Диаграмма состояний (рис. 26) отражает наличие у триггера двух устойчивых состояний и условия перехода из одного состояния в другое. Словарь триггера (табл. 8) даёт ту же информацию в аналитической форме и является инструментом проектирования схем, содержащих триггеры.
Рис. 26. Диаграммы состояний (графы переходов) для JK-триггера
Таблица 8
| Переход | J | K |
| 0→0 | 0 |  |
| 0→1 | 1 | |
| 1→0 | | 1 |
| 1→1 | | 0 |
Важным способом описания функционирования триггеров (как и других автоматов) являются временные диаграммы, отражающие не только логическое функционирование схемы, но и её поведение во времени. Это поведение другими способами описания работы триггеров не отображается, и поэтому в ряде случаев временные диаграммы незаменимы. Временные диаграммы соответствуют той картине, которую можно наблюдать на экране осциллографа или логического анализатора (рис. 27).
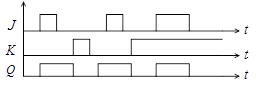
Рис. 27. Временные диаграммы работы асинхронного JK-триггера
На практике временные диаграммы чаще всего изображаются схематично, без осей координат (с целью упрощения графических изображений).
Приведённое выше описание относится к асинхронному JK-триггеру, изменение состояний которого происходит под действием входных сигналов J и K.
На практике чаще всего используются синхронные триггеры, отличающиеся наличием дополнительного, так называемого синхронизирующего входа С (от англ. слова clock – тактировать).
Восприятие входных сигналов J и K у синхронного триггера происходит только при наличии активного уровня сигнала на входе С.
Работу такого триггера можно проиллюстрировать временной диаграммой (рис. 28).
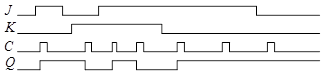
Рис. 28. Временные диаграммы работы синхронного JK-триггера
2.2.3 Получение управляющих сигналов
Переходы кодируются в соответствии с таблицей переходов для JK – триггера (Таблица 3). Полученные функции возбуждения для каждого триггера представлены в Приложении 2.
2.2.4 Построение схем функций возбуждения
Осуществим минимизацию каждого из входных сигналов триггеров. При этом «» можно доопределять «0» или «1» исходя из целесообразности минимизации. На основе полученных минимизированных функций, построим схемы функции возбуждения для каждого входа.