Курсовая работа: Теоремы Силова

Так как , то - объединение нескольких правых смежных классов G по . Поэтому , откуда . В случае имеем . Равенства и эквивалентны. Получаем

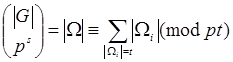
(- некоторый элемент из G) и, стало быть, - подгруппа порядка . Орбита исчерпывается некоторым числом левых смежных классов группы G по .

Обратно: каждая подгруппа порядка приводит к орбите длины t. Различные подгруппы с приводят к различным орбитам , поскольку из следует , откуда и . Таким образом, имеется взаимно однозначное соответствие между подгруппами порядка и орбитами длины t. Тогда сравнение записывается как

Где следовало бы написать , чтобы подчеркнуть зависимость от G.

Если взять за G циклическую группу порядка , то для неё и поэтому

Так как левые часть сравнений по одному и тому же модулю совпадают, то имеем

А это и даёт искомое сравнение

Получим полезное уточнение теорем Силова.

Теорема 4.

Справедливы следующие утверждения:

1).силовская p-подгруппа P группы G нормальна в G тогда и только тогда, когда

2).конечная группа G порядка является прямым произведением своих силовских - подгрупп в точности тогда, когда все эти подгруппы нормальны в G.

Доказательство.

1).Все силовские подгруппы, отвечающие данному простому делителю р порядка , по второй теореме Силова сопряжены, и если P–одна из них, то

нормальна в G

2).Если - прямое произведение своих силовских подгрупп, то нормальна в G как любой прямой множитель. Значит условие нормальности необходимо.

Пусть теперь нормальна в G, , т.е. . Заметим, что . Стало быть, , а отсюда для любых имеем

Т.е. элементы и перестановочны.

Представим, что единичный элемент записан в виде , где - элемент порядка . Положив и воспользовавшись перестановочностью получим

Но так как а и взаимно просты, то . Это верно при любом j, и, стало быть, равенство возможно лишь при

С другой стороны, каждый элемент порядка , записывается в виде , , . Достаточно положить , где показатели определяются условиями

теорема силов конечная группа

,