Курсовая работа: Теоремы Силова

,

что, как было показано выше, влечёт равенства

, т.е. .

Итак, каждый элемент группы G записывается, и притом единственным образом в виде .

Замечание

Нормальная силовская p-подгруппа P группы G характеристична в G, т.е. инвариантна при действии любого автоморфизма . Действительно, , поэтому - силовская р-подгруппа, и, стало быть, , если . Аналоги силовских подгрупп прослеживаются в алгебраических структурах, далёких от конечных групп.

Следствие

Если все делители | G | , кроме 1, после деления на p дают остаток, отличный от единицы, то в G есть единственная силовская p-подгруппа и она является нормальной (и даже характеристической).

Примеры силовских подгрупп.

Пример 1.

Аддитивная группа кольца вычетов разлагается в прямое произведение своих силовских p-подгрупп, которые являются циклическими подгруппами порядков , если n имеет каноническое разложение n=.

Пример 2.

Силовские p-подгруппы симметрических групп. Как мы знаем, Каков максимальный показатель e(n), при котором делит n!? В последовательности 1,2,…,n кратными p будут числа p,2p,…,kp, где , поэтому . Так как 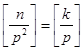, то 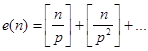Удобно разложить n по основанию p: , тогда

Рассмотрим сначала группы , когда n степень p. Пусть в уже найдена силовская p-подгруппа, т.е. подгруппа порядка . Построим по ней в подгруппу порядка . Для этого разобьём переставляемые символы 1,2,…, на последовательные отрезки длины . Если 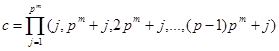и x – подстановка на символах i-го отрезка, то легко сообразить, что - подстановка на символах (i+1)-го отрезка (сложение по модулю p). Отсюда видно, что подгруппа, порождённая подгруппами , является из прямым произведением, и, стало быть, подгруппа , порожденная подгруппой и элементом с, изоморфна сплетению . Подгруппа - искомая, так как .

Одновременно мы видим, что силовская p-подгруппа в изоморфна последовательному сплетению (…( циклической группы с самой собою mраз.

Теперь пусть n произвольно. Разобьём символы 1,...,n на одноэлементных, р-элементных и т.д. отрезков. На каждом из этих отрезков рассмотрим симметрическую группу – она будет некоторой степени , а в ней возьмём силовскую p-подгруппу, построенную как выше. Так как эти подгруппы действуют на непересекающихся множествах, то их порождение является их прямым произведением, а потому имеет порядок

Следовательно, - силовская p-подгруппа в . Из построения видно, что она изоморфна прямому произведению нескольких последовательных сплетений типа (…(.

Пример 3

Рассмотрим общие линейные группы над конечными полями. Пусть p – простое число, m, n – целые числа и . Покажем, что - силовская p-подгруппа группы . Посчитаем порядки этих групп.

Какие n-ки над полем могут быть первой строкой невырожденной матрицы? Очевидно, любые, кроме нулевой, т. е. штук. Если первая строка выбрана, то в качестве второй строки можно взять любую, не пропорциональную первой; таких строк. Если две первые строки уже выбраны, то в качестве третьей можно взять любую строку, не зависящую линейно от первых двух; это дает возможностей. И так далее. Значит, .

Так как угловые элементы матриц пробегают независимо друг от друга всё поле, а всего угловых мест , то . Из сравнения порядков мы видим, что - силовская p-подгруппа группы .

Нахождение силовской подгруппы.

Проблема нахождения силовской подгруппы данной группы является важной задачей вычислительной теории групп. Для групп перестановок Уильям Кантор доказал, что силовская p-подгруппа может быть найдена за время, полиномиальное от размера задачи (в данном случае это порядок группы, помноженный на количество порождающих элементов).

ГЛАВА 2.РЕШЕНИЕ ЗАДАЧ С ПРИМЕНЕНИЕМ ТЕОРЕМ СИЛОВА

Задача 1.

Докажем, что группа порядка 350 не может быть простой.

Решение

, значит, силовская 5-подгруппа имеет порядок 25. N5 должно делить 14 и сравнимо с 1 по модулю 5. Этим условиям удовлетворяет только единица. Значит, в G одна силовская 5-подгруппа, а значит, она нормальна, и поэтому G не может быть простой.