Курсовая работа: Теплопроводность жидкостей и газов

16

22,5

0,1765

0,1411

0,0237

0,0226

403

86,5

68,2

35,6

0,190

0,167

0,158

6,9

3. Теплопроводность жидкостей и газов

Теплопроводность , один из видов переноса теплоты (энергии теплового движения микрочастиц) от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры. При теплопроводности перенос энергии в теле осуществляется в результате непосредственной передачи энергии от частиц (молекул, атомов, электронов), обладающих большей энергией, частицам с меньшей энергией.

Отклонения от закона Фурье могут появиться при очень больших значениях grad T (например, в сильных ударных волнах), при низких температурах (для жидкого гелия Не) и при высоких температурах порядка десятков и сотен тысяч градусов, когда в газах перенос энергии осуществляется не только в результате межатомных столкновений, но в основном за счёт излучения (лучистая теплопроводность). В разреженных газах, когда l сравнимо с расстоянием L между стенками, ограничивающими объём газа, молекулы чаще сталкиваются со стенками, чем между собой. При этом нарушается условие применимости закона Фурье, и само понятие локальной температуры газа теряет смысл. В этом случае рассматривают не процесс теплопроводности в газе, а теплообмен между телами, находящимися в газовой среде.

4. Теплопроводность газов

Для идеального газа, состоящего из твёрдых сферических молекул диаметром d, согласно кинетической теории газов, справедливо следующее выражение

(3.4)

где — плотность газа, c_v — теплоёмкость единицы массы газа при постоянном объёме, V — средняя скорость движения молекул. Поскольку J пропорциональна 1/р, а ~ р (р — давление газа), то Т. такого газа не зависит от давления. Кроме того, коэффициент теплопроводности и вязкости связаны соотношением: . В случае газа, состоящего из многоатомных молекул, существенный вклад в дают внутренние степени свободы молекул, что учитывает соотношение:

,

где = ср/c_v , ср — теплоёмкость при постоянном давлении. В реальных газах коэффициент теплопроводности — довольно сложная функция температуры и давления, причём с ростом Т и р значение возрастает. Для газовых смесей может быть как больше, так и меньше коэффициента теплопроводности компонентов смеси, то есть теплопроводности - нелинейная функция состава.

Если газ неравномерно нагрет , т. е. температура в одной его части выше или ниже, чем в другой, то наблюдается выравнивание температуры: более нагретая часть охлаждается, тогда, как более холодная нагревается.

Очевидно, что это связано с потоком тепла от более нагретой части газа к более холодной. Это явление возникновения потока тепла в газе называется теплопроводностью, В любом теле, в частности в газе, предоставленном самому себе, теплопроводность приводит к выравниванию температур, и этот процесс, конечно, нестационарный. Но часто встречаются и случаи, когда разность температур искусственно поддерживается постоянной.

Например, в электрической лампе накаливания газ, находящийся непосредственно около накаленной нити, имеет высокую температуру (равную температуре самой нити), тогда как газ, прилегающий к стенкам стеклянного баллона лампы, обладает значительно более низкой температурой. Через некоторое время после включения лампы устанавливается постоянная разность температур между нитью и стенками. Это постоянство обеспечивается, с одной стороны, электрической энергией, подводимой к нити из электрической сети, с другой стороны — отдачей тепла от стенок лампы к окружающему ее воздуху. При этих условиях в газе, находящемся в лампе, устанавливается стационарный, т. е. не изменяющийся со временем, поток тепла. Установившаяся стационарная разность температур зависит от теплопроводности газа (для лампы накаливания надо иметь в виду, что кроме отвода тепла через газ в данном частном случае отвод тепла происходит главным образом в результате излучения).

В приведенном примере лампы расчет потока тепла представляет большие трудности, связанные со сложной формой нити и сосуда, вследствие чего распределение температуры в газе тоже оказывается весьма сложным.

Чтобы найти количественные закономерности, характеризующие процесс теплопроводности, мы рассмотрим более простую задачу

Пусть вдоль какого-нибудь направления в газе, например, вдоль оси X, температура меняется от точки к точке, т. е. является функцией v. в то время как в плоскости, перпендикулярной к этой оси, температура всюду одинакова

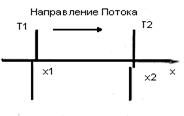
Изменение температуры вдоль оси X характеризуется градиентом температуры .