Курсовая работа: Цифровые автоматы

0

1

0

1

0

1

0

0

0

0

0

1

0

1

0

Задание:

а) произвести логическое сложение чисел А и С:

Ú	0|000000100110011
	0|000000001011011
0|000000101111011

б) произвести логическое умножение чисел А и С:

&	0|000000100110011
	0|000000001011011
0|000000000010011

в) произвести сложение чисел А и С по модулю 2.

Å	0|000000100110011
	0|000000001011011
0|000000101101000

г) произвести логический сдвиг: влево для чисел А и –А, вправо для С и –С

A	–A
0|000000100110011	1|111111011001101	Число
0|000001001100110	1|111110110011010	Результат сдвига влево

C	–C
0|000000001011011	1|111111110100101	Число
0|000000000101101	0|111111111010010	Результат сдвига вправо

д) произвести логический циклический сдвиг: влево для чисел А и –А, вправо для чисел С и –С

A	–A
0|000000100110011	1|111111011001101	Число
0|000010011001100	1|111101100110100	Результат сдвига влево на 2 бита

C	–C
0|000000001011011	1|111111110100101	Число
0|000000000010110	0|011111111101001	Результат сдвига вправо на 2 бита

e) произвести арифметический сдвиг: влево для чисел А и –А, вправо для чисел С и –С

A	–A
0|000000100110011	1|111111011001101	Число
0|000001001100110	1|111110110011010	Результат сдвига влево

C	–C
0|000000001011011	1|111111110100101	Число
0|000000000101101	1|011111111010010	Результат сдвига вправо

Глава 2. Методы контроля работы ЦА

2.1 Корректирующая способность кодов

При работе ЦА могут произойти те или иные сбои, приводящие к искажению информации. Поэтому при проектировании ЦА должны предусматриваться средства, позволяющие контролировать, выявлять и исправлять возникающие ошибки. Решение всех задач контроля становится возможным только при наличии определенной избыточности информации, которая сопровождает основную информацию. Иначе говоря, при представлении числа в каком-либо коде, необходимо предусмотретьв этом коде дополнительные (контрольные) разряды.

Систематический код – это код, содержащий в себе информационные и контрольные разряды. В контрольные разряды записывается некоторая информация об исходном числе, поэтому систематический код обладает избыточностью.

При этом абсолютная избыточность будет выражаться количеством контрольных разрядов – k , а относительная избыточность – , где m – количество информационных разрядов.

Понятие корректирующей способности кода связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Корректирующая способность кода связана понятием кодового расстояния.

Кодовое расстояние (Хемингово расстояние) d для кодовых комбинаций A и B определяется как вес такой третьей комбинации, которая получается сложением исходных комбинаций по модулю 2. Вес кодовой комбинации V – это количество единиц содержащихся в кодовой комбинации.

Например, A=100111001 и B=011011100. Отсюда веса кодовых комбинаций будут равны: V(A)=5, V(B)=5. Кодовая комбинация C=A+B=111100101, вес этой кодовой комбинации равен V(C)=6. Таким образом кодовое расстояние для A и B – d(A,B)=V(C)=6.

В любой позиционной системе счисления минимальное кодовое расстояние равно 1. В теории кодирования показано, что систематический код обладает способностью обнаружения ошибки только тогда, когда код расстояния для него больше или равен 2t. Следовательно, , где t – кратность обнаруживаемых ошибок. Это означает, что между соседними кодовыми комбинациями должна существовать, по крайней мере одна кодовая комбинация.

2.2 Метод четности / нечетности. Коды Хеминга

Если в математическом коде выделен один контрольный разряд, то к каждому двоичному числу добавляется один избыточный разряд. В этот разряд записывается 1 или 0 с таким условием, чтобы сумма цифр по модулю 2 была равна 0 для случая четности или 1 для случая нечетности. Появление ошибки в кодировании обнруживается по нарушению четности / нечетности. При таком кодировании допускается, что может возникнуть только одна ошибка.

Пример реализации метода четности:

Число	Контрольный разряд	Проверка
10101011	1	0
11001010	0	0
10010001	1	0
11001011	0	1 – ошибка

Можно представить и несколько видоизмененный способ контроля по методу четности / нечетности. Длинное слово разбивается на группы, каждая из которых содержит n разрядов. Контрольные разряды – k , выделяются всем группам по строкам и столбцам согласно следующей схеме:

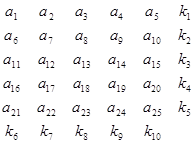
Увеличение избыточности приводит к тому, что появляется возможность не только обнаружить ошибку, но и исправить ее.