Курсовая работа: Управление развитием предприятия

(5)

Задача ставится так: необходимо найти значения qj ,q2 ,q3, такие, которые
обеспечивают Е (t) > Етр (6)

Здесь - требуемая эффективность использования фонда развития предприятия.

Условие (5) может выполняться при различных сочетаниях значений ql q2, q3, т.е. условия (4) и (5) не обеспечивают определенности решения задачи. Для этого нужно ввести дополнительное условие: придадим максимальную неопределенность возможным значениям qi,q2, q3.

В качестве меры неопределенности используем энтропию совокупности значений q1, q2, q3, которая может быть записана так:

Тогда задача принимает вид: найти такие q1, q2, q3, при которых:

max

(7)

Задача может быть решена известным в математике методом неопределенных множителей Лагранжа. Согласно этому методу составляется функция:

Где ] и являются множителями Лагранжа.

Затем определяют частные производные по qi и и которые приравниваются к нулю, т.е.

i=1,2,3

Система (8) состоит из 3 уравнений с 5 неизвестными q1 q2, q3, ,. Решение системы уравнений может быть получено с использованием стандартных математических пакетов программ (в нашем случае с помощью пакета MAPLE). Систему (8) можно решить, и преобразовав ее к более простому виду.

Первые 3 уравнения могут быть переписаны так:

i=1,2,3

Отсюда (9)

Подставим qj в 4 и 5 уравнения системы (7) и получим:

(10)

Поделим левую и правую части (10) на левую и правую части (11):

(12)

Если задать требуемую эффективность етр использования фонда развития, то

(12) будет представлять собой уравнение с одним неизвестным xl

Упростим соотношение (12), для этого проинтегрируем правую и левую части по ,
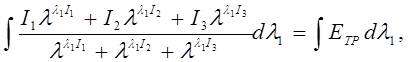