Курсовая работа: Устойчивость прямоугольных пластин судового корпуса

Это число "m" должно, очевидно, удовлетворять тому условию, при котором при подстановке в правую часть формулы вместо m величины (m+ 1) и (m - 1) значение скобки будет увеличиваться. Это условие запишется в виде:

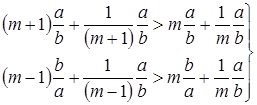(14)

Из выражения (15) можно получить:

(15)

Последние неравенства показывают, что на длине пластины образуется следующее число полуволн:

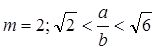
Расчёт эйлеровых значений сжимающих усилий прямоугольной свободно опёртой по контуру пластины, сжатой вдоль короткой стороны опорного контура (16)

Для стальной пластины с параметрами Е=2,15*10⁶ кг/см² ; μ=0,3 , сжатой вдоль короткой стороны опорного контура, эйлерово напряжение определяется:

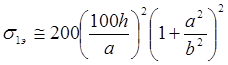(16)

Для определения эйлерова напряжения пластины с параметрами Е=210·10³ МПа = 2,1·10⁶ кг/см² и μ=0,3 вдоль короткой стороны необходимо формулу (21) домножить на Е/Е_ст , тогда:

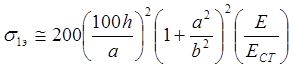
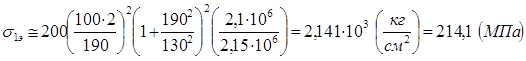
Расчёт эйлеровых значений сжимающих усилий прямоугольной свободно опёртой по контуру пластины, сжатой вдоль длинной стороны опорного контура (17)

Для стальной пластины с параметрами Е=2,15*10⁶ кг/см² ; μ=0,3 , сжатой вдоль длинной стороны опорного контура, эйлерово напряжение определяется:

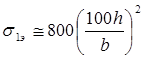(17)

Для определения эйлерова напряжения пластины с параметрами Е=210·10³ МПа = 2,1·10⁶ кг/см² и μ=0,3 вдоль длинной стороны необходимо формулу (21) домножить на Е/Е_ст , тогда:

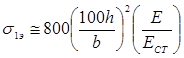
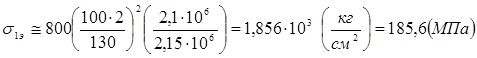
Устойчивость пластин, свободно опертых по двум кромкам. Решение в виде ординарного тригонометрического ряда. Расчётная схема (рис.3)

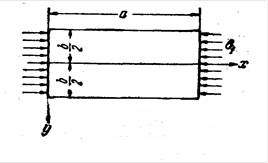
Рис.3

Решение для упругой поверхности пластины, у которой кромки х = const свободно оперты на жесткий контур (18)

Рассмотрим пластину, у которой кромки х = const свободно оперты на жесткий контур, и загруженную сжимающими усилиями в направлении оси ох . Решение для упругой поверхности такой пластины можно искать в виде ординарного тригонометрического ряда:

(18)

Дифференциальное уравнение нейтрального равновесия пластины (24). Дифференциальное уравнение, которому должны удовлетворять функции (20)

Дифференциальное уравнение нейтрального равновесия пластины:

(19)

где Т₁ = - σ₁ h

Функции должны удовлетворять дифференциальному уравнению: