Курсовая работа: Устойчивость прямоугольных пластин судового корпуса

Общий интеграл для функций (21)

На основании решения, полученного при рассмотрении изгиба пластин, свободно опертых по двум кромкам, формула общего интеграла для функций запишется в виде:

(21)

Где

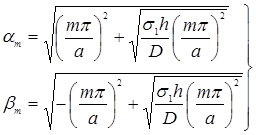(22)

Граничные условия для функции, для пластины, жестко заделанной по своим продольным кромкам, (25)

Рассматриваемое решение позволяет исследовать устойчивость пластин при различных условиях закрепления на кромках, параллельных сжимающей нагрузке.

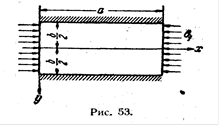
Продольные кромки жестко заделаны (рис.4).

Рис.4

В этом случае граничные условия для упругой поверхности пластины w (х, у) будут:

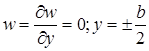(23)

Учитывая, что ожидаемая форма потери устойчивости будет симметрична относительно оси ох, можем в общем интеграле функции сохранить лишь четные члены, т.е. записать его в виде

(24)

и подчинить это выражение граничным условиям на кромке .

Учитывая выражения (18) и (23), получим следующие граничные условия для функции:

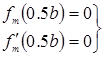(25)

Система линейных однородных уравнений относительно постоянных A_m и С _m (26)

Подчиняя выражение (24) условиям (25), получим

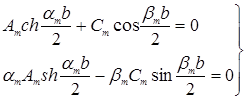(26)

Определение эйлеровых напряжений пластины, жестко заделанной по своим продольным кромкам (27)

Определение эйлеровых напряжений пластины, жестко заделанной по своим продольным кромкам, по формуле:

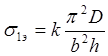(27)

Где k выбирается из таблицы в зависимости от соотношения сторон пластины b: a

b: а	0,4	0,5	0,6	0,7	0,8	0,9	1,0
k	9,44	7,69	7,05	7,00	7,29	7,83	7,69

Примем коэффициент k=7,00 тогда

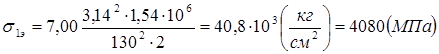
Устойчивость пластины, одна продольная кромка которой свободно оперта, другая совершенно свободна. Расчётная схема (рис.5)

Одна продольная кромка пластины свободно оперта, другая совершенно свободна