Курсовая работа: Устройство формирования управляющих сигналов
в) достаточно ли низок уровень высокочастотной помехи по сравнению с уровнем полезного выходного сигнала?
Если хотя бы с точки зрения одного из этих критериев работу дифференцирующего звена нельзя признать удовлетворительной, наметить меры по устранению обнаруженного недостатка. Выяснить при этом, не приведут ли намеченные меры к ухудшению качества по другим критериям. Оформить результаты анализа в виде предварительных выводов. Если достижение нужного качества при использовании заданной простейшей схемы дифференцирующего устройства затруднительно или невозможно, продумать и предложить улучшенный вариант (варианты) схемы, которая должна при этом оставаться пассивной. Улучшение должно состоять в том, что отмеченный недостаток в работе простейшей схемы должен устраняться, но не за счет ухудшения других необходимых качеств.
4. Вывести (в общем виде) выражения для АЧХ и ФЧХ новой, скорректированной схемы устройства. Произвести выбор тех параметров схемы, которые в данном случае могут быть признаны неизменяемыми. Если в схеме используется индуктивность, которая не может быть реализована в виде стандартного элемента, выпускаемого промышленностью, определить конструктивные параметры катушки (число витков, сечение провода), обладающей приемлемым значением индуктивности, используя для этой цели кольцевой магнитопровод, выполненный из феррита с относительной магнитной проницаемостью μr , с размерами, указанными на рис.5.
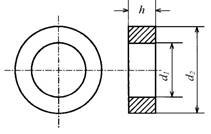
Рис. 5. Линейные размеры кольцевого магнитопровода
Активное сопротивление обмотки должно быть рассчитано и включено в схему замещения дифференцирующего устройства.
Определить алгоритм выбора изменяемого параметра (параметров) устройства, удовлетворяющего выбранным критериям качества (приемлемый уровень выходного сигнала при достаточной точности дифференцирования и низком уровне помех). Определить величину изменяемого параметра (параметров) схемы.
5. Построить графики АЧХ и ФЧХ дифференцирующего устройства с учетом выбранных величин ее параметров, определить с их помощью выходное напряжение ![]() . Проанализировать качество дифференцирования, построив и сравнив графики идеальной производной
. Проанализировать качество дифференцирования, построив и сравнив графики идеальной производной ![]() (где u1 (t)) -полезный входной сигнал без учета помехи) и выходного сигнала u2 (t), оценив степень их совпадения. Коэффициент т следует выбрать так, чтобы оба напряжения были соизмеримы по уровню.
(где u1 (t)) -полезный входной сигнал без учета помехи) и выходного сигнала u2 (t), оценив степень их совпадения. Коэффициент т следует выбрать так, чтобы оба напряжения были соизмеримы по уровню.
Оформить этот анализ в виде окончательных выводов.
Исходные данные
Таблица 1 - Исходные данные
| Вар. | Входной сигнал u1 (t), B |
| 6 |
|
Таблица 2 - Данные
| Вар. | d1, мм | d2, мм | h, мм | μr | dпр, мм | ||
| 6 | 14 | 22 | 4 | 1400 | 0,2 | 1,85 | 0,042 |
Анализ частотных характеристик идеального дифференцирующего устройства
Амплитудно- и фазо-частотные характеристики идеального дифференцирующего устройства
 |  |
|
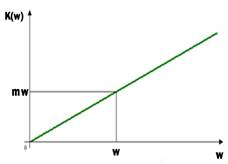
Рис. 6 и 7 - АЧХ идеального дифференцирующего устройства (отношение модулей амплитуд входного и выходного) | ФЧХ идеального дифференцирующего устройства (разность начальных фаз напряжений входного и выходного сигнала ) |
Идеальное дифференцирующее устройство – это устройство, способное осуществлять операцию дифференцирования в любом диапазоне частот спектра входного сигнала, причём с абсолютной точностью. Технически идеальной считается операция, когда входное u1 (t) и выходное ![]() напряжения идеального дифференцирующего звена связаны соотношением:
напряжения идеального дифференцирующего звена связаны соотношением:
![]() ,
,
где m=const – некоторый произвольный коэффициент пропорциональности (обычно m<<1). При этом уровень помехи выходного сигнала должен быть приемлемо низким.
Входной сигнал как синусоидальная функция в общем виде, и в комплексную форме. ![]()
Выходной сигнал как синусоидальная функция в общем виде, и в комплексную форме. ![]()
Амплитудно-частотная характеристика (АЧХ) идеального дифференцирующего устройства есть отношение модулей амплитуд входного и выходного напряжений(![]()
Фазо-частотная характеристика (ФЧХ) равна разности начальных фаз напряжений![]()
Производная входного сигнала, домноженная на коэффициент пропорциональности m

Вычислим в общем виде АЧХ и ФЧХ идеального дифференцирующего устройства. ![]() ;
;
Рассмотрим входной сигнал u1 (t), как синусоидальную функцию в общем виде, и переведём её в комплексную форму:
Таким образом,