Курсовая работа: Устройство формирования управляющих сигналов

Проведём анализ формул для расчёта АЧХ и ФЧХ r-L-c цепочки с точки зрения критериев, описанных в техническом задании. Целью анализа будет установление интервала частот Δω, в котором может находиться резонансная частота ω₀ , и при этом будут выполняться все три критерия качества. При анализе можно пренебречь активным сопротивлением катушки r_k , т.к. r_k <<r . Поэтому можно считать, что оно не оказывает существенного влияния на характер АЧХ и ФЧХ.

C учётом сказанного, перепишем формулы (4) и (5), подставив в них зависимости:

и (c).

Получим:

(6)

(7)

При расчете интервала частот Δω, можно принять следующие обозначения:

ω₀₁ - минимально-необходимое значение резонансной частоты ω₀ , обеспечивающее соответствие первому критерию качества,

ω₀₂ - максимально возможное значение ω₀ , обеспечивающее выполнение требований второго критерия;

ω₀₃ - максимально возможное значение ω₀ , обеспечивающее выполнение требований третьего критерия.

1) Расчёт резонансной частоты ω₀ с точки зрения критерия минимального уровня полезного сигнала на выходе.

Составим неравенство, исходя из условия, что минимально-необходимым можно принять сигнал u₂ (t), у которого амплитуда первой гармоники не меньше 1мВ: (8).

Подставив выражение для K(ω) из формулы (6), составим и решим неравенство:

, где , .

Решая это неравенство относительно ω₀₁ , получим:

ω₀₁ – любое значение (9). Расчёт резонансной частоты ω₀ с точки зрения критерия точности дифференцирования выходного сигнала.

В качестве опорных неравенств, воспользуемся неравенствами (10) и (11), которые приведены в техническом задании:

(10) и (11)

Подставим из выражения (6) в неравенство (10) значения K₍₁₎ =K(ω₁ ) и K₍₂₎ =K(ω₂ ), получим:

Здесь , , . Решая это неравенство относительно ω₀₂ , получим:

ω₀₂ – любое значение (12). Подставим из формулы (7) в неравенство (11) значение , получим:

.

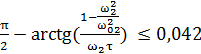Решая это неравенство относительно ω₀₂ , получим: ω₀₂ ≥2797,5 рад/с (13)

2) Расчёт резонансной частоты ω₀ с точки зрения критерия помехозащищённости r - L - c цепочки.

Для расчёта помехозащищённости, воспользуемся условием неравенства (6):

(3)

Здесь и . Подставим эти значения в неравенство (3), используя формулу (6). Получим:

;