Курсовая работа: Увеличение электрической прочности ускоряющего промежутка электронного источника при наличии пучка

q – элементарный заряд

С учётом вышесказанного получим:

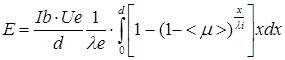(5.1)

Чтобы найти концентрацию нейтралов и их температуру в пределах цилиндра радиуса R – n_b , T_b – необходимо записать уравнения баланса частиц и энергий.

Поток частиц из цилиндра Ф_out :

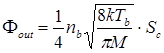(5.2)

Поток частиц в цилиндр Ф_in :

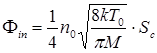(5.3)

где S_с = 2pR² + 2pRd – площадь поверхности цилиндра;

M – масса нейтрала; k – постоянная Больцмана;

n_b и n₀ – концентрация нейтралов в цилиндре и за его пределами;

T_b и T₀ – температуры нейтралов в цилиндре и за его пределами.

Если Ф_in = Ф_out , то из формул (5.2–5.3) получим:

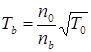(5.4)

Энергия, выносимая из цилиндра W_out :

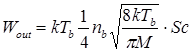(5.5)

Энергия, вносимая в цилиндр W_in :

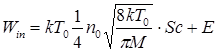, (5.6)

где E находится по формуле (5.1)

Если W_in = W_out , то, подставив в формулу (5.5) выражение (5.4), получим:

, (5.7)

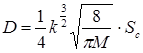где (5.8)

Так как (P – давление газа за пределами цилиндра), то получим:

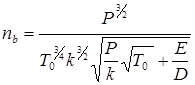, или

если Pвыражено в Торр. (5.9)

Таким образом, при увеличении энергии ионов имеет место снижение концентрации нейтралов. В свою очередь, энергия ионов увеличивается за счёт роста тока пучка. Результаты модели в полной мере соответствуют зависимостям, полученным экспериментальным путем. Локальный нагрев газа электронным пучком ведёт к увеличению электрической прочности ускоряющего промежутка плазменного источника электронов в присутствии пучка в ускоряющем промежутке, в форвакуумном диапазоне давлений.

6. РАСЧЁТ И ОБРАБОТКА РЕЗУЛЬТАТОВ

Исходные данные

P = 60 ¸ 160 мТорр (давление газа вне пучка)