Курсовая работа: Вейвлет-анализ сигналов и его применение

Многомасштабное редактирование

Как уже неоднократно подчеркивалось, основу различных применений вейлетов составляет возможность простого и быстрого изменения разрешения сигнала, преобразованного с помощью DWT. Но эта черта вейвлетов негде так не очевидна как при многомасштабном редактировании изображений и трехмерных моделей. Дело в том, что при многомасштабном редактировании изменение разрешения редактируемого объекта происходит интерактивно, что особенно хорошо выявляет описанные преимущества вейвлетов. Рисунок 3.6 иллюстрирует идею многомасштабного редактирования.

вейвлет преобразование редактирование дискретный

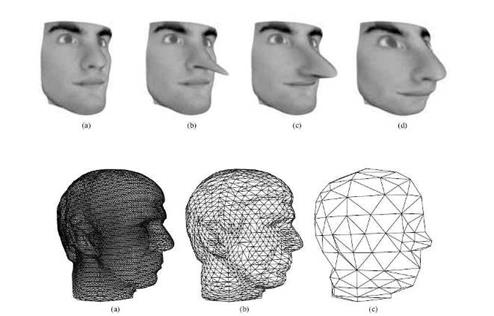
Рисунок 3.2 – Многомасштабное редактирование трехмерной модели

Как мы можем видеть на рисунке 3.2 представлена трехмерная модель головы человека, при этом модель представлена в трех разных разрешениях, переход между этими разрешениями, как нетрудно догадаться, осуществляется с помощью добавления детализирующих, вейвлет коэффициентов. При этом само редактирование происходит по-разному при разных разрешениях. По сути дела с уменьшением разрешения модели увеличивается радиус (масштаб) влияния редактора.

Заключение

Список приложений вейвлетов чрезвычайно широк, причем области их применения не ограничиваются цифровой обработкой сигналов, но охватывают также физическое моделирование, численные методы и другие области науки.

На мой взгляд, такой интерес к вейвлетам вызван двумя факторами, во-первых, они сделали то, что долгое время не удавалось никому – предоставить альтернативу спектральному анализу и предоставить качественный инструмент анализа нестационарных сигналов, во-вторых, они представляют сигнал в пространственно-временной области, что существенно проще для понимания человеком.

Перечень использованных источников

1. И.М. Дремин, О.В. Иванов, В.А. Нечитайло. Вейвлеты и их использование. – Успехи физических наук, 2001

2. Wavelet Digest – www.wavelet.org

3. Br. Vidakovic, P. Mueller. Wavelets for kids – Duke University.

4. А. Переберин. Многомасшабные методы синтеза и анализа изображений – Москва, 2001.

5. А. Петров. Вейвлеты и их приложения – Рыбинск, РГАТА 2007