Курсовая работа: Верхний центральный показатель некоторой линейной системы
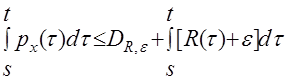 ,
,
где ![]() - константа, общая для всех
- константа, общая для всех ![]() и
и ![]() , но, вообще говоря, зависящая от выбора R и
, но, вообще говоря, зависящая от выбора R и ![]() >0.
>0.
Определение 2 [1, с.103]: совокупность всех верхних функций называется верхним классом семейства P (обозначим через N=N (P)).
Определение 3 [1, с.534 ]: число
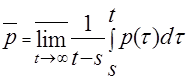
называется верхним средним значением функции p (t).
Определение 4 [1, с.103]: число
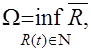
где ![]() - верхнее среднее значение функции R (t), называется верхним центральным числом семейства P. Оно будет обозначаться также
- верхнее среднее значение функции R (t), называется верхним центральным числом семейства P. Оно будет обозначаться также ![]() .
.
Докажем следующее утверждение: если семейство состоит из двух функций ![]() и при этом
и при этом ![]() , то верхний класс семейства P можно считать состоящим из одной функции
, то верхний класс семейства P можно считать состоящим из одной функции ![]() , и
, и ![]() .
.
Неравенство ![]() означает, что
означает, что
![]()
и для любого ![]() существует такая константа
существует такая константа ![]() , что
, что
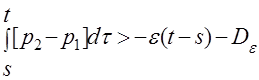
Или
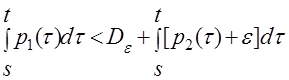
![]() (1)
(1)
Аналогичное неравенство для функции ![]() очевидно
очевидно
 .
.
Согласно определения 1 ![]() является верхней функцией для семейства
является верхней функцией для семейства
![]() .
.
Докажем равенство
![]() .
.
Если существует такая верхняя функция ![]() , что
, что ![]() для всех
для всех ![]() , то эта функция одна образует верхний класс и
, то эта функция одна образует верхний класс и ![]() [1, с.104].
[1, с.104].
Найдем такую верхнюю функцию ![]() , что
, что ![]() .
.
Рассмотрим интегралы

Разделим последнее неравенство на (t-s), получим

Устремив ![]() и вычислив верхний предел при
и вычислив верхний предел при ![]() , получим
, получим