Курсовая работа: Верхний центральный показатель некоторой линейной системы

или

Итак, имеем

Значит, .

Так как - верхняя функция, то .

2. Верхний центральный показатель линейной системы

Пусть дана система

(2)

и - ее решение.

Рассмотрим семейство функций

,,

Определение 5 [1, с.116]: Функция R (t) называется верхней для системы (2), если она ограничена, измерима и осуществляет оценку

,

Где

- норма матрицы Коши линейной системы.

Совокупность всех верхних функций называется верхним классом системы (2), а число

верхним центральным показателем линейной системы.

Диагональная система

имеет матрицу Коши

с нормой

.

Поэтому верхний центральный показатель диагональной системы совпадает с верхним центральным числом конечного семейства P={} [1, с.118].

Найдем верхний центральный показатель следующей системы

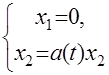
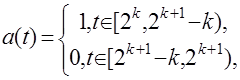(3)

где k=0, 1, 2,….

Верхний центральный показатель системы (3) совпадает с верхним центральным числом конечного семейства