Курсовая работа: Виды теплообмена

Промежуточные температуры типа Т_X можно найти из уравнения (1.6).

Предполагается, что при параллельном соединении термических сопротивлений R₂ и R₃ тепловой поток остается одномерным; если же сопротивления R₂ и R₃ заметно отличаются друг от друга, могут стать существенными двумерные эффекты.

1.3 Цилиндрические координаты

Из задач теплопроводности для тел цилиндрической формы чаще всего встречается задача о кондуктивном тепловом потоке через длинный полый цилиндр (рисунок 1.3). Известно, что температура внутренней поверхности цилиндра равна T_i , а температура наружной поверхности Т_о . Стационарное распределение температуры в твердом теле с постоянными теплофизическими свойствами при отсутствии внутреннего тепловыделения определяется решением уравнения теплопроводности при двух граничных условиях: Т(r_i )=T_i ; Т(r₀ )=Т₀ . Решение для местной температуры Т(r) имеет вид

(1.8)

Выражение (1.8) записывается в безразмерной форме следующим образом:

. (1.9)

Следовательно, температура изменяется в радиальном направлении по логарифмическому закону.

Поскольку распределение температуры известно, тепловой поток вдоль радиуса цилиндра можно найти с помощью закона Фурье для цилиндрической системы координат,

(1.10)

где — длина цилиндра.

Дифференцируя распределение температуры (1.8) и подставляя полученный результат в соотношение (1.10), получаем

(1.11)

Выражение (1.11) записано в форме закона Ома, и знаменатель представляет собой термическое сопротивление полого цилиндра:

(1.12)

Используем интегральную форму представленного термического сопротивления. Получаем

Принципы последовательного и параллельного соединения термических сопротивлений в цепь, справедливые для плоской стенки в прямоугольной системе координат, можно применить и для задачи о теплопроводности в полом цилиндре. Предположим, например, что жидкость течет в трубе, покрытой теплоизоляционным материалом (рисунок 1.4). Известно, что средняя температура жидкости равна T₁ , а температура внешней поверхности изоляции Т₂ . Характеристики материала трубы обозначены индексом 1, а изоляции—индексом 2. Конвективное термическое сопротивление жидкости определяется формулой (1.01). Конвективное термическое сопротивление жидкости нужно соединить последовательно с двумя кондуктивными термическими сопротивлениями для двух твердых материалов, поскольку тепловой поток распространяется последовательно через каждый из этих материалов.

Тепловой поток в этой задаче выражается соотношением:

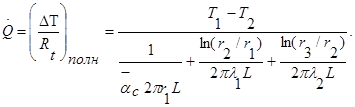(1.13)

Термическое сопротивление, входящее в соотношение (1.13), является суммой всех термических сопротивлений между двумя известными температурами. Если известны температуры Т₁ и Т₂ , то полное сопротивление должно равняться сумме только кондуктивных сопротивлений трубы и изоляции. Температура Т_x при известном тепловом потоке находится из соотношения

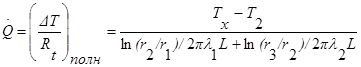(1.14)

1.4 Сферические координаты

Распределение температуры и тепловой поток для полого шара определяются таким же образом, как для полого цилиндра и плоской стенки. Стационарное одномерное распределение температуры при отсутствии внутреннего тепловыделения определяется из решения упрощенного уравнения теплопроводности, записанного в сферических координатах. Это уравнение имеет вид

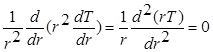
Предполагаем, что граничными условиями являются заданные температуры внутренней и наружной поверхности шара (рисунок 1.5.): Т(r_i )=T_i ; Т(r₀ )=Т₀ . В таком случае распределение температуры в полом шаре определяется соотношением

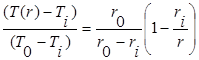(1.15)

Следовательно, температура полого шара изменяется в радиальном направлении по гиперболическому закону.

Тепловой поток через стенку шара можно найти, применяя закон Фурье к соотношению (1.15). В итоге получаем

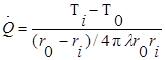(1.16)

Таким образом, термическое сопротивление стенки шара выражается формулой