Курсовая работа: Виды теплообмена

Для интегрального представления имеем

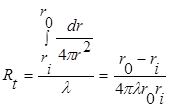
Использование интегрального представления более универсально, не требует математического описания, интегрирования дифференциального уравнения, определения констант и т. д.

1.5 Суммарный коэффициент теплопередачи

Если в задаче теплообмена участвует несколько термических сопротивлений, соединенных последовательно, параллельно или комбинированно, удобно ввести суммарный коэффициент теплопередачи, или суммарную удельную тепловую проводимость. Суммарный коэффициент теплопередачи обозначается через К и определяется формулой

(1.18)

Величина K играет ту же роль, что и коэффициент конвективной теплоотдачи a . И К , и a имеют размерность Вт/(м^2. град). Если соотношение (1.18) сравнить с равенством

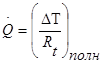, (1.19)

то видно, что К можно выразить через полное термическое сопротивление цепи:

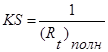(1.20)

В качестве примера использования суммарного коэффициента теплопередачи рассмотрим трехслойную, плоскую стенку, показанную на рисунке 1.2. Величина К в этой задаче находится по формуле

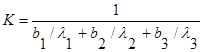
В этом примере площади поперечного сечения всех трех материалов одинаковы, поэтому нет сомнений, какую площадь нужно использовать в соотношении (1.20). Однако, если площади для каждого термического сопротивления различны, нужно быть последовательными при выборе площади, входящей в соотношение (1.20). Случаю переменной площади соответствует задача о многослойной цилиндрической стенке с последовательным соединением термических сопротивлений. Величину KS для тепловой цепи (рисунок 1.4) можно определить из формулы

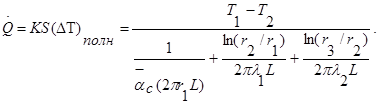или

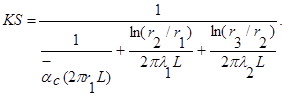
Отметим, что произведение KS постоянно, но величина K зависит от выбора соответствующей площади. Предположим, например, что за характерную площадь мы приняли площадь внутренней поверхности трубы S_i =2 p r₁ L . В таком случае величина K , рассчитанная по S _i , равна

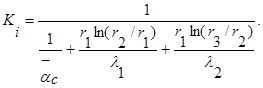
Если величина K рассчитана по площади наружной поверхности трубы S₀ = 2 p r₃ L , то

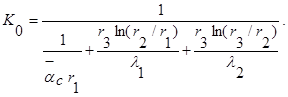
Несмотря на то, что значения K _i и K _o различны, произведение KS всегда постоянно: K _i S _i = K _o S _o .

2. ВЫНУЖДЕННЫЙ КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

Уметь рассчитывать конвективный тепловой поток нужно не только при течениях в каналах, но и при обтекании пластин, цилиндров, сфер и пучков труб, что важно для инженерных приложений.

2.1 Плоская пластина

Теплообмен при обтекании плоской пластины показывает, что для данной жидкости среднее число Нуссельта прежде всего зависит от числа Рейнольдса, вычисленного по скорости невозмущенного течения и длине пластины в направлении потока. В некоторых случаях бывает необходимо знать местный коэффициент теплоотдачи, и тогда характерным размером, используемым в числах Нуссельта и Рейнольдса, будет расстояние от передней кромки. В инженерных расчетах локальное число Нуссельта при ламинарном обтекании плоской пластины (Re_x < 5-10⁵ ) определяют по формуле

, (2.1)

тогда как среднее число Нуссельта определяют по формуле

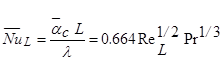,. (2.2 )

Средний коэффициент теплоотдачи в формуле (2.1) получают интегрированием

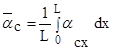(2.3 )

При турбулентном обтекании (Rе_L .>5^. 10⁵ ) на части пластины, непосредственно следующей за передней кромкой, течение ламинарное, и лишь далее оно становится турбулентным. Локальное значение числа Нуссельта при любом х за местом смены режима течения, т. е. при х > x_с , определяется по формуле

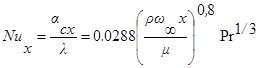, (2.4 )

в то время как среднее его значение, если переход происходит при Re_x =5-10⁵ , равно