Курсовая работа: Задача о коммивояжере и ее обобщения

Величины h_i и g_j называются константами приведения. Оптимальная последовательность городов для задачи коммивояжера с матрицей С⁽²⁾ будет, очевидно, такой же, как и для исходной задачи, а длины пути для варианта номера s в обоих задачах будут связаны между собой равенством

(5.2)

где

(5. 3)

т. Е. d ₀ равна сумме констант приведения.

Обозначим через l * решение задачи коммивояжера,т.е.

где минимум берется по всем вариантам s , удовлетворяющим условию (α) Тогда величина d ₀ будет простейшей нижней оценкой решения:

(5.4)

Будем рассматривать теперь задачу коммивояжера с матрицей С⁽²⁾ которую мы будем называть приведенной матрицей.

Рассмотрим путь, содержащий непосредственный переход из города номера i в город номера j , тогда для путиs , содержащего этот переход, мы будем иметь, очевидно, следующую нижнюю оценку:

Следовательно, для тех переходов, для которых = 0, мы будем иметь снова оценку (5.4). Естественно ожидать, что кратчайший путь содержит один из таких переходов — примем это соображение в качестве рабочей гипотезы. Рассмотрим один из переходов, для которого =0, и обозначим через множество всех тех путей, которые не содержат перехода из i в j .

Так как из города i мы должны куда-то выйти, то множество содержит один из переходов i → k , где k ≠ j ; так как в город номера j мы должны прийти, то множество содержит переход m →j , где т ≠ i .

Следовательно, некоторый путь l_s из множества ( ij ), содержащий переходы i → k и m →j , будет иметь следующую нижнюю оценку:

Обозначим через

Тогда очевидно, что для любого l_s из множества путей мы будем иметь оценку

(5.5)

Мы предполагаем исключить некоторое множество вариантов , поэтому мы заинтересованы выбрать такой переход i → j , для которого оценка (5.5) была бы самой высокой. Другими словами, среди нулевых элементов матрицы С⁽²⁾ выберем тот, для которого максимально. Это число обозначим через Таким образом, все множество возможных вариантов мы разбили на два множества I₁ и I₂ . Для путей из множества I₁ , мы имеем оценку (5.4). Для путей из множества I₂ оценка будет следующей:

(5.6)

Рассмотрим теперь множество I₁ и матрицу С ⁽²⁾ . Так как все пути, принадлежащие этому множеству, содержат переход i → j , то для егоисследования нам достаточно рассмотреть задачу коммивояжера, в которой города номеров i и j совпадают. Размерность этой задачи будет уже равна N – 1, а ее матрица получится из матрицы С⁽²⁾ вычеркиванием столбца номера j и строки но мера i .

Поскольку i → j невозможен, то элемент принимаем равным бесконечности.

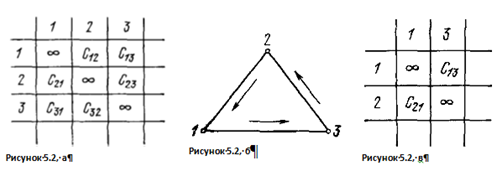
Рассмотрим случай N=3 (Рисунок 5.2, а ), и предположим, что мы рассматриваем тот вариант, который содержит переход 3 → 2. Тогда задача коммивояжера после вычеркивания третьей строки и второго столбца вырождается в тривиальную. Ее матрица изображена на рисунке 5.2, в. В этом случае мы имеем единственный путь, и его длина будет, очевидно, равна сумме

Итак, если в результате вычеркивания строки номера i и столбца номера j мы получим матрицу второго порядка, то задачу можно считать решенной.

Пусть теперь N >3. После вычеркивания мы получим матрицу порядок