Курсовая работа: Задача о коммивояжере и ее обобщения

С этой матрицей ( N — 1)- гопорядка совершим процеурру приведения. Матрицу, которую таким образом получим, обозначим через С⁽³⁾ , а через d ⁽¹⁾ – сумму ее констант приведения. Тогда для l_s I₁ , мы будем иметь оценку

(5.7)

На этом первый шаг алгоритма закончен. В результате одного шага мы разбили множество всех возможных вариантов на два множества I₁ и I₂ и для путей, принадлежащих этим множествам, мы получили оценки (5.7) и (5.6) (Рисунок 5.3)

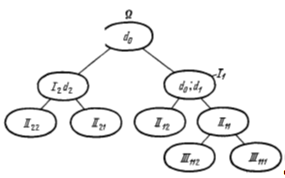
Рис.5.3

Введем понятие стандартной операции, которую мы будем обозначать символом Этим термином мы назовем процедуру разбиения произвольного множества вариантов Ω с приведенной матрицей N – п- гопорядка С^{( n + 2)} и оценкой d_ω на два множества. Одно из этих множеств состоит из всех тех путей, которые содержат переход из города номер s в город номер l и имеют нижнюю оценку d . Другое множество состоит из всех путей, не содержащих этого перехода и имеющих в качестве нижней оценки число d_k . Стандартную операцию можно представить в форме следующей блок-схемы (см. Рисунок 5.4).

задача коммивояжер решение алгоритм обобщение

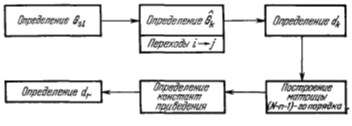
Рисунок 5.4

Итак, первый шаг метода ветвей и границ состоит в проведении стандартной операции над исходным множеством Ω. На следующем шаге мы продолжаем развивать дерево возможных вариантов. Сначала мы сравниваем две оценки d ₁ и d ₂ и для последующего анализа выбираем то из множеств I₁ или I₂ , для которого соответствующая оценка меньше.

Предположим, что

d ₁ < d ₂ ;

тогда над множеством I₁ с матрицей С^{(3 )} мы совершим стандартную операцию. В результате мы разобьем множество возможных вариантов I₁ на два подмножества II₁₁ и II₁₂ , первое из которых содержит некоторый переход i ₁ → j ₁ а другое содержит все пути, не имеющие непосредственною перехода из города i ₁ в город j ₁ . Еще раз повторим рассмотренную выше процедуру: для каждого из нулевых элементов матрицы С^{(3 )} построим число

Определим значение

и элемент матрицы С^{(3 )} , для которого достигается это значение. Если l_s II₁₂ , то

(5.8)

Затем в матрице С ⁽³⁾ вычеркиваем строку номера i ₁ и столбец номера j ₁ , полагаем и над полученной матрицей совершаем операцию приведения. В результате мы найдем новые константы приведения. Их сумму обозначим через d ^{( II )} и в заключение находим оценку d ₁₁ для элементов множества II₁₁ .

Если l_s II₁₁ , то

(5.9)

На этом второй шаг алгоритма ветвей и границ закончен. Мы разбили множество вариантов I₁ на два множества, II₁₁ и II₁₂ , и для элементов этих множеств получили нижние оценки (5.9) и (5.8), соответственно.

Теперь мы должны сравнить оценку (5.9) с оценкой (5.6) для элементов множества I₂ , которое мы исключили из рассмотрения на предыдущем шаге. Если окажется, что d ₂ > d ₁₁ ,

то мы переходим к третьему шагу, который состоит в применении стандартной операции к множествуII₁₁ . (Если размерность матрицы при этом равна двум, то, как мы видели выше, процесс заканчивается.)

Если окажется, что d ₁₁ > d ₂ , то множеством вариантов с оптимальной нижней оценкой будет множество I₂ . Другими словами, теперь будем предполагать, что наиболее короткий путь содержится среди элементов множества I₂ — множества всех вариантов, не содержащих перехода i → j . Следовательно, матрица, характеризующая это множество, получается из матрицы С ⁽²⁾ заменой величины на ∞. Над этим множеством мы производим стандартную операцию и разбиваем его на два множества II₂₁ и II₂₂ с оценками d ₂₁ и d ₂₂ , соответственно. Одновременно мы выделяем переход k → l , который содержит все варианты множества II₂₁ . Затем мы снова сравниваем все оценки d ₁₁ , d ₁₂ , d ₂₁ и d ₂₂ и выбираем то из множеств, для которого оценка будет наименьшей. Над выбранным множеством совершаем стандартную операцию и т. Д. Так мы продолжаем до тех пор, пока очередная матрица не будет иметь порядок (2x2). В этом случае, как мы видели, расчет заканчивается — мы получаем задачу коммивояжера для двух городов (Рисунок 5.5), и длина единственного маршрута будет

Итак, мы получили некоторую цепочку (ветвь) переходов, длину которой мы вычислили. Сам порядок построения этой цепочки показывает, что ее длина — наименьшая среди всех ветвей дерева, изображенного на рисунке 5.3.

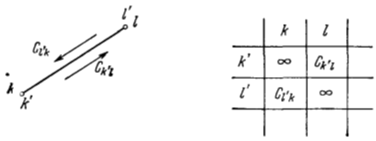
Рисунок 5.5

6. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЗАДАЧИ КОММИВОЯЖЕРА

Задача коммивояжера имеет ряд практических применений. Как следует из самого названия задачи, ее можно использовать для составления маршрута человека, который должен посетить ряд пунктов и, в конце концов, вернуться в исходный пункт. Например, задача коммивояжера использовалась для составления маршрутов лиц, занимающихся выемкой монет из таксофонов. В этом случае вершинами являются места установки таксофонов и "базовый пункт". Стоимостью каждого ребра (отрезка маршрута) является время в пути между двумя точками (вершинами) на маршруте.

Задача о производстве красок. Имеется производственная линия для производства n красок разного цвета; обозначим эти краски номерами 1,2… n . Всю производственную линию будем считать одним процессором.. Будем считать также, что единовременно процессор производит только одну краску, поэтому краски нужно производить в некотором порядке. Поскольку производство циклическое, то краски надо производить в циклическом порядке (j₁ ,j₂ ,..,j_n ,j₁ ). После окончания производства краски i и перед началом производства краски j надо отмыть оборудование от краски i . Для этого требуется время C [i,j ]. Очевидно, что C [i,j ] зависит как от i , так и от j , и что, вообще говоря,C [i,j ] ≠ C[j,i ]. При некотором выбранном порядке придется на цикл производства красок потратить время, где t_k - чистое время производства k -ой краски (не считая переналадок). Однако вторая сумма в правой части постоянна, поэтому полное время на цикл производства минимизируется вместе с общим временем на переналадку.