Лабораторная работа: Анализ устойчивости электротехнической системы

Из рис.1 видно, что пара комплексно-сопряженных корней s ₃ = a ₃ + j·β ₃ и s ₄ = a ₄ - j·β ₄ при изменении k му в заданной области переходят из левой полуплоскости в правую полуплоскость. Следовательно, по изменению этой пары корней можно определить критический коэффициент усиления магнитного усилителя. Графический способ определения критического коэффициента магнитного усилителя, показан на рис. 2.

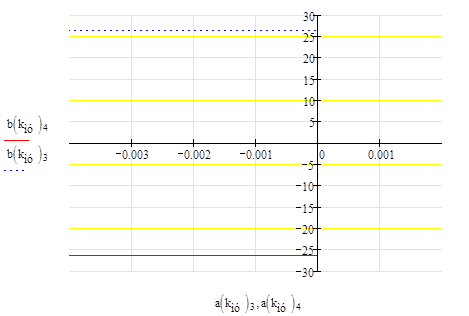
Рис.2. Графический способ определения критического коэффициента передачи магнитного усилителя.

Табличный метод определения критического коэффициента передачи магнитного усилителя.

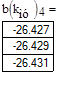K му=11,18

2.3. Использование алгебраического критерия Рауса - Гурвица для анализа устойчивости системы

Для анализа устойчивости и определения критического коэффициента передачи прямого канала усиления системы в функции k му рассматриваемой системы с помощью алгебраического критерия устойчивости Рауса-Гурвица воспользуемся детерминантами D ₄ и D ₂ , рекомендуемые Льенара – Шипара, так как характеристическое уравнение имеет пятый порядок.

а) детерминант D ₂ :

б) детерминант D ₄ .

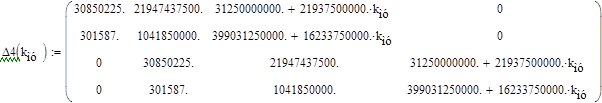Как видим, детерминант ∆₂ > 0 , а ∆4 при коэффициенте передачи магнитного усилителя k му = 11,186980560011235894 равен нулю, т.е. система находится на грани устойчивости. Следовательно, критический коэффициент передачи магнитного усилителя равен k мукр =11,186980560011235894

Для того, чтобы убедиться что это действительно критическое значение коэффициента магнитного усилителя, определим корни характеристического уравнения для найденного коэффициента магнитного усилителя.

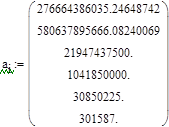
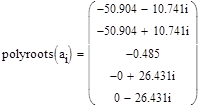
Как видим, характеристический полином имеет пару чисто мнимых корней, следовательно, система находится на грани устойчивости.

2.4 Построение годографов Найквиста по передаточной функции разомкнутой системы заданной в виде полинома

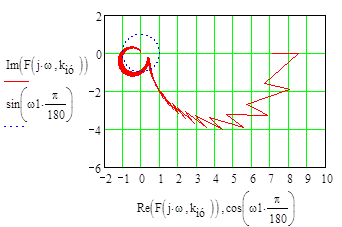
Частотный критерий Найквиста при исследовании устойчивости автоматических систем базируется на амплитудно-фазовой частотной характеристики разомкнутой системы и может быть сформулирован следующим образом:

если характеристическое уравнение разомкнутой системы n -го порядка имеет k корней с положительной вещественной частью ( k = 0, 1, ….. n ) и n - k корней с отрицательной вещественной частью, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф амплитудно-фазовой частотной характеристики разомкнутой системы (годограф Найквиста) охватывал точку (-1, j 0) комплексной плоскости на угол k π , или что тоже самое, охватывал точку (-1, j 0) в положительном направлении, т.е. против часовой стрелки, k раз.

Для частного случая, когда характеристическое уравнение разомкнутой системы не имеет корней с положительной вещественной частью (k= 0),т.е. , когда она устойчива в разомкнутом состоянии, критерий Найквиста формулируется следующим образом:

система автоматического регулирования устойчива в замкнутом состоянии, если амплитудно-фазовая частотная характеристика разомкнутой системы при изменении частоты от 0 до ∞ не охватывает точку комплексной плоскости с координатами (-1, j 0).

Критерий устойчивости Найквиста удобно применять для систем с обратной связью, особенно систем высокого порядка.

Для построения годографа Найквиста воспользуемся передаточной функцией разомкнутой системы в символьном виде из Практического занятия №5

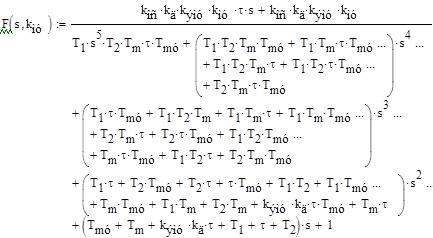
Запишем ее в символьно-цифровом виде для заданных параметров всех элементов системы, кроме коэффициента передачи магнитного усилителя:

Запишем уравнение амплитудно-фазовой частотной характеристики,, выделим вещественную и мнимые частотные характеристики и построим семейство годографов Найквиста в функции частоты и коэффициента передачи магнитного усилителя.

Построения графика амплитудно-фазовой частотной характеристики в Math С ad