Лабораторная работа: Будування математичної моделі економічної задачі і розвязання її за допомогою графічного метода
Х = { хі }, і = 1 ÷ n = 5,
С = (5, 3, 0, 0, 0),
 1 2 1 0 0
1 2 1 0 0
А = 2 5 0 1 0
2,236068 3 0 0 1
В = (50, 75, 50).
Як бачимо, вихідна задача максимізації цільової функції Z в нормальній формі (1) набула канонічного вигляду (2) за рахунок перетворення обмежень-нерівностей на обмеження-рівності шляхом введення балансових змінних.
Завдання 2
Розв'язати задачу лінійного програмування, сформульовану в Завданні 1, графічним методом:
Z = 3x1 + 2x2 → max
![]() 2х1 + х2 ≤ 4,
2х1 + х2 ≤ 4,
х1 + 2х2 ≤ 5, (1)
х1 ≥ 0, х2 ≥ 0.
Розв'язок
Використовуючи крайні значення знаків ≤ обмежень несуворих нерівностей, тобто знаки =, побудуємо такі три графіки:
1) х1 = - x2 /2 + 2,
2) х1 = -2x2 + 5,
3) x1 = Z - 2x2 /3
Ці графіки показані на рис. 1, на якому многокутник розв’язків, як видно, обмежений знизу (оскільки в системі обмежень (1) фігурують знаки ≤) тільки додатною чвертю декартової системи х1,2 ≥ 0.
На цьому рисунку цільова функція показана штриховою лiнiєю, яка, залежно від величини Z, може переміщуватися паралельно сама собі. Стрілкою з буквою n на рис. 1 позначений напрямок градієнта цільової функції (тобто напрямок збільшення Z). Зрозуміло, що її максимум знаходиться в точці перетину ліній обмежень 1) і 2), в якій х1 = 1 > 0, х2 = 2 > 0. Це й є графічний розв'язок задачі. При цьому цільова функція буде мати таке значення:
Z = 3*1 + 2*2 = 7.
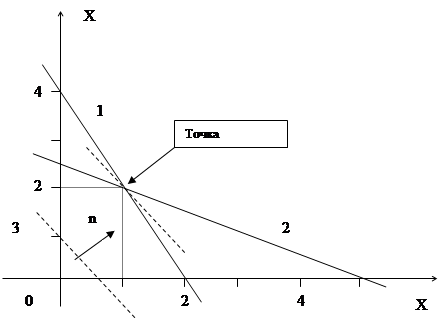 |
Рисунок 1. Графік до розв’язання Завдання 2
Завдання 3
Розв'язати систему лінійних рівнянь методом повного виключення змінних (метод Гаусса) з використанням розрахункових таблиць:
![]() 2х1 + х2 - х3 - х4 = 2
2х1 + х2 - х3 - х4 = 2
4х1 + х3 - 7х4 = 3
2х1 - 3х2 + х4 = 1
Розв'язок
Взагалі кажучи, ця недовизначена система може або мати безліч розв'язків, або не мати жодного (тобто бути несумісною ). Для з'ясування цього застосуємо метод Гаусса (точніше, Жордана-Гаусса), який реалізуємо у вигляді таблиць 2 – 4. В таблиці 1 вміщені вихідні дані.
Таблиця 1. Вихідна матриця системи
|
А1 |
К-во Просмотров: 553
Бесплатно скачать Лабораторная работа: Будування математичної моделі економічної задачі і розвязання її за допомогою графічного метода
|