Лабораторная работа: ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения системы дифференциальных уравнений

вар

Ко э ф ф и ц и е н т ы с и с т е м ы д и ф ф е р н е ц и а л ь н ы х у р а в н е н и й Начальные условия а₁₁ а₁₂ а₁₃ а₁₄ а₂₁ а₂₂ а₂₃ а₂₄ а₃₁ а₃₂ а₃₃ а₃₄ а₄₁ а₄₂ а₄₃ а₄₄ b₀ b₁ b₂ b₃ х₀ (0) х₁ (0) х₂ (0) х₃ (0) 8 -2,4 1,4 1,6 -1,8 -2,6 -12 0,6 4,0 -0,8 -0,85 -0,1 0,2 0,4 1,2 1,0 -1,5 0,1 0,2 0 0,6 0 0 -0.8 5.1

Электротехническая система описывается заданной системой линейных дифференциальных уравнений с 4 искомыми функциями х0(t), x1(t),x2(t), x3(t):

Матрицы системы:

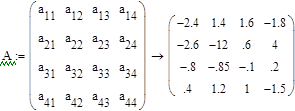
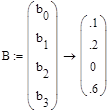
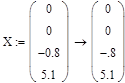
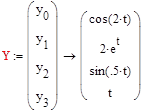
2. Решение системы дифференциальных уравнений, заданной в нормальной форме Коши

2.1 Теоретическое обоснование

Можно записать в виде матричного дифференциального уравнения:

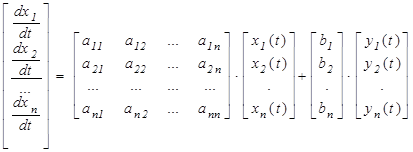
или на основании правила дифференцирования матриц:

Совокупность решений системы дифференциальных уравнений будем искать в форме

здесь - общее решение однородной системы дифференциальных уравнений

X(t) - частное решение неоднородной системы дифференциальных уравнений .

Общее решение однородной системы дифференциальных уравнений

Для определения общего решения системы дифференциальных уравнений необходимо:

· найти собственные значения λ_i матрицы А, используя выражение:

· найти переходную матрицу:

где Р – матрица, составленная из собственных векторов v_i матрицы А, которые определяются из выражения:

Аv_i = λ_i v_i i = 1,2..n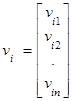 - одно из произвольных значений вектора-столбца (обычно принимают v_{i 1} = 1)

Тогда 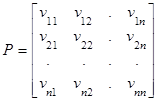причем - диагональная матрица.

Общее решение однородной системы дифференциальных уравнений будет иметь вид:

Частное решение неоднородной системы дифференциальных уравнений ищется:

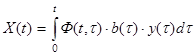
Общее решение неоднородной системы дифференциальных уравнений тогда будет иметь вид: