Лабораторная работа: ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения системы дифференциальных уравнений

Также применим обратное проеобразование Лапласа , нажав ключевое слово invlaplace на панели Символика.

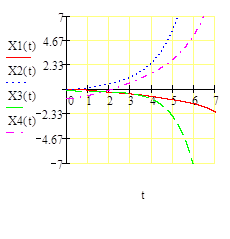
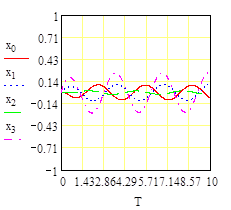
Рисунок 2.2.Графики изменения переменных состояния системы при нулевых начальных условиях и присутствии внешнего воздействия, полученные с помощью преобразования Лапласа.

Как видно графики совпадают.

2.5 Частное решение неоднородной системы дифференциальных уравнений при заданном внешнем воздействии y = cos (2 t ) и нулевых начальных условиях

2.5.1 Решение с помощью переходной матрицы

В качестве примера рассмотрим случай, если на систему действует воздействие одного вида, например y=cos(2t) .

Определим аналитические выражения изменения независимых переменных системы и их графическое представление при заданных внешних воздействиях и нулевых начальных условиях.

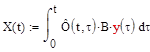
пусть

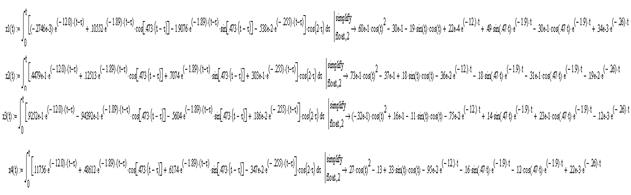
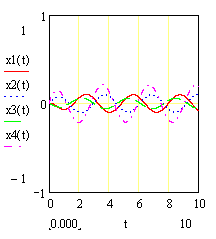
Рисунок 3.1. Графики изменения переменных состояния системы при при y(t)=cos(2t) и нулевых начальных условиях, полученные способом решения с использованием переходной матрицы.

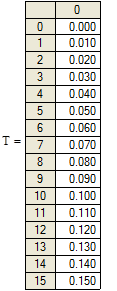
2.5.2 Численный метод решения системы дифференциальных уравнений при нулевых начальных условиях и заданном внешнем воздействии y = cos (2 t ) c помощью MATHCAD

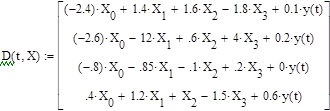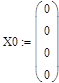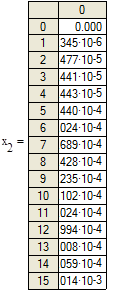
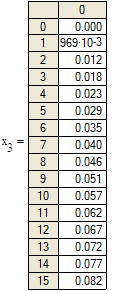
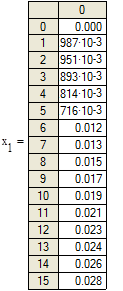
Рисунок 3.2. Графики изменения переменных состояния системы при нулевых начальных условиях и воздействии y=cos(2t)

Как видно из графиков решения совпадают.

2.5.3 Решение системы дифференциальных уравнений при нулевых начальных условиях и заданном внешнем воздействии y = cos (2 t ) c помощью преобразования Лапласа

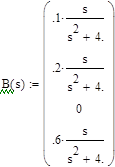
Применив обратное преобразование Лапласа (invlaplace) получим значения x(t), графическое изображение которых на рисунке 3.3. Рисунок совпадает с двумя полученными ранее.

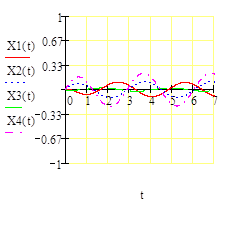
Рисунок 3.3. Графики изменения переменных состояния системы при при y(t)=cos(2t) и нулевых начальных условиях, полученные с помощью преобразования Лапласа.

2.6 Решение неоднородной системы дифференциальных уравнений при заданном внешнем воздействии и начальных условиях

2.6.1 Решение с помощью функции MATHCAD

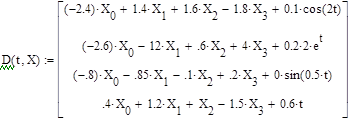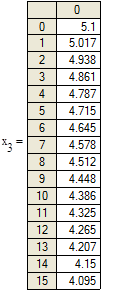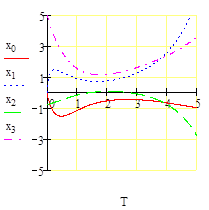
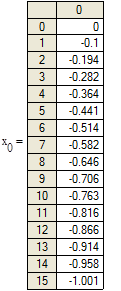
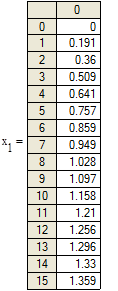
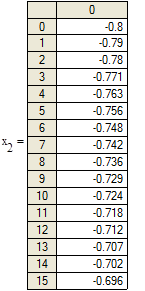
Рисунок 4.1. Графики изменения переменных состояния системы при заданных начальных условиях и воздействии, полученных с помощью функции MATHCAD.

2.6.2 Решение с помощью преобразования Лапласа