Лабораторная работа: ЭВМ с использованием математического пакета MathCad в среде Windows 98 для решения системы дифференциальных уравнений

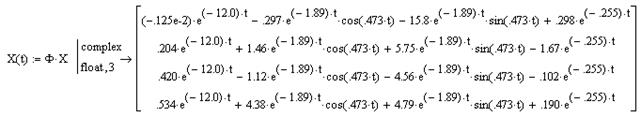
Тогда получим 4 решения:

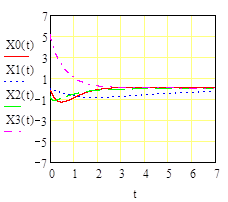
Рисунок 1.1. Графики изменения переменных состояния системы при заданных начальных условиях и отсутствии внешнего воздействия.

2.3.2 Определение аналитических зависимостей изменения переменных состояния системы при заданных начальных условиях и отсутствии внешнего воздействия с использованием функции Mathcad

СПРАВКА: В Mathcad 11 имеются три встроенные функции, которые позволяют решать поставленную в форме (2—3) задачу Коши различными численными методами.

· rkfixed(y0, t0, t1, M, D) — метод Рунге-Кутты с фиксированным шагом,

· Rkadapt(y0, t0, t1, M, D) — метод Рунге-Кутты с переменным шагом;

· Buistoer(y0, t0, t1, M, D) — метод Булирша-Штера;

o у0 — вектор начальных значений в точке to размера NXI;

o t0 — начальная точка расчета,

o t1 — конечная точка расчета,

o M — число шагов, на которых численный метод находит решение;

o D — векторная функция размера NXI двух аргументов — скалярного t и векторного у При этом у — искомая векторная функция аргумента t того же размера NXI.

Таким образом, воспользуемся функцией Rkadapt (y0, t0, t1, M, D) -получим матрицу решения системы дифференциальных уравнений численным методом Рунге-Кута на интервале от t0 до t1 при Mшагах решения и правыми частями уравнений, записанными в D. Тогда решение уравнения динамики электротехнической системы с помощью встроенной функции Rkadapt выглядит так:

Зададим интервал интегрирования t0 - t1, количество шагов интегрирования М, вектор заданных начальных условий X0 и правую часть дифференциального уравнения y(t):

Сформируем матрицу системы дифференциальных уравнений:

Применим функцию:

-Интервал времени.

-Значение искомой координаты.

Рисунок 1.2. Графики изменения переменных состояния системы при заданных начальных условиях и отсутствии внешнего воздействия, полученные с помощью MATHCAD.

Как видно из графического представления решения, график полученный с помощью переходной функции такой же как график, полученный с помощью функции MATHCAD.

2.3.3 Определение аналитических зависимостей изменения переменных состояния системы при заданных начальных условиях и отсутствии внешнего воздействия с использованием преобразования Лапласа

Заданную систему уравнений преобразуем по Лапласу и найдем переходную матрицу и изображение по Лапласу переменной состояния системы:

На основании переходной матрицы определим изображение и оригинал переменных состояния систем: