Система, содержащая функции конъюнкции, дизъюнкции и отрицания, является функционально полной. К ним относятся Стрелка Пирса и Штрих Шеффера.

Таблица 1

Аргументы	Обозначения	Наименование
: 0 0 1 1
: 0 1 0 1
1 1 0 0		Отрицание или инверсия
0 1 1 1		Дизъюнкция
0 0 0 1		Конъюнкция
0 1 1 0		Сложение по модулю 2(неравнозначность)
1 0 0 0		Стрелка Пирса
1 1 1 0		Штрих Шеффера
1 0 0 1		Равнозначность

Основные теоремы алгебры логики

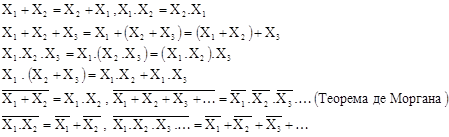
Элементарные логические операции над двоичными переменными реализуются электронными схемами – логическими элементами. Один и тот же закон преобразования информации можно рассматривать, используя различные типы комбинаций ЛЭ и связи между ними. На рис. 7 показана функционально полная система совокупности элементов И, ИЛИ, НЕ. На рис. 8 показана реализация логических операций НЕ, ИЛИ, И только с помощью одного элемента И-НЕ.

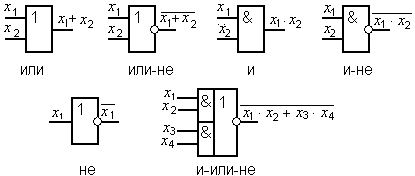
Рис. 7. Функционально полная система элементов И, ИЛИ, НЕ

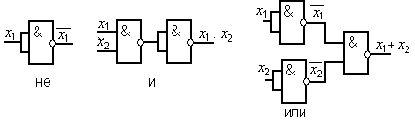
Рис. 8. Реализация логических операций в базисе И-НЕ

Синтез переключательной функции

Любая логическая функция может быть представлена в дизъюнктивной или конъюнктивной нормальной форме (ДНФ или КНФ). ДНФ представляет собой логическую сумму элементарных произведений, каждое из которых аргумент или его отрицание входит не более одного раза.

Если каждое слагаемое содержит все переменные или их отрицания, то имеет стандартную форму (СДНФ): совершенную дизъюнктивную нормальную форму (СДНФ), которая является одним из вариантов алгебраического способа задания булевых функций.

Синтез переключательной функции состоит в получении ее ДНФ или КНФ и получении минимальной формы функций. При синтезе схем выполняется задача построения схем с использованием минимального числа элементов в базисе И-НЕ или ИЛИ-НЕ.

Синтез комбинационных схем с одним выходом осуществляется в следующей последовательности.

На первом этапе осуществляется запись условий функционирования в виде логической функции, словесно в виде таблиц истинности, структурных формул.

На втором этапе осуществляется запись и минимизация структурной формулы, т.е. осуществляется приведение переключательной функции к совершенной нормальной форме и ее минимизация.

На третьем этапе осуществляется запись минимизированной структурной формулы на заданном базисе. Чаще всего в универсальных базисах И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.

На четвертом этапе составляется структурная схема, определяющая число элементов и необходимые соединения между ними. Рассмотрим пример синтеза комбинационной схемы. Пусть заданы условия функционирования в виде таблицы истинности (табл. 2, вариант 13). Записываем структурную формулу в виде СДНФ по таблице истинности

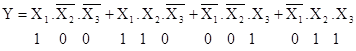(1)

Число слагаемых определяется числом единичных наборов (Y = 1) таблицы истинности, а число сомножителей определяется числом независимых переменных, входящих в рассматриваемые наборы.

Для реализации этой функции необходимо иметь 4 трехвходовых элемента И и один четырехвходовый элемент ИЛИ.

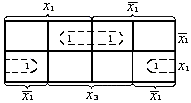
Минимизацию структурной формулы (1) произведем при помощи диаграммы Вейча (рис. 9). Получаем выражение

которое также можно получить, применив правило склеивания,

Полученную минимизированную структурную формулу можно также представить в виде

Производим преобразования структурных формул (2) и (4) в базисе И-НЕ, используя законы инверсии (формулы де Моргана):

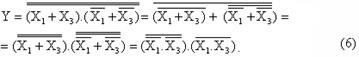
Структурные схемы, составленные по формулам (2), (5) и (6), приведены на рис. 10. Видим, что после минимизации для реализации функции требуется меньшее число логических элементов.