Лабораторная работа: Изучение тонких линз и сферических зеркал
Лабораторная работа
Изучение тонких линз и сферических зеркал
Введение
Цель работы: изучение методов определения фокусных расстояний линз и зеркал; наблюдение и оценка их аберраций
Широкое применение линз и сферических зеркал объясняется их свойством, при определенных условиях, превращать расходящиеся гомоцентрические пучки лучей в гомоцентрические сходящиеся пучки, т.е. давать изображения предмета, подобные объекту. Собирающие (рассеивающие) свойства линз и зеркал количественно описываются формулой зеркала и формулой линзы, которые легко получить из формулы преломляющей поверхности (1):
(1)
Здесь а1 – расстояние от источника света L до вершины S сферической поверхности радиусом R, разделяющей две среды с показателями преломления n1 и n2 (рис.1), а2 – расстояние от вершины до изображения источника света L¢.
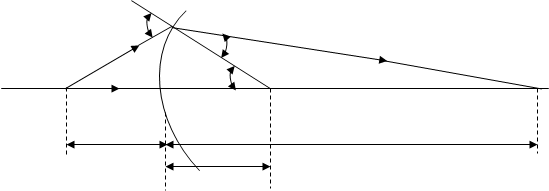n1 A n2
i
r
L S j C L¢
a1 a2
R
Рис.1
Видно, что положение изображения L¢, т.е. а2 – однозначно определяется через а1 , n1 , n2 , R, т.е. точка изображается точкой. При выводе этой формулы принято следующее правило знаков: все расстояния отсчитываются от вершины поверхности S и считаются положительными по ходу луча. Если источник L расположен далеко от поверхности, т.е. а1 = ¥, лучи падают на сферическую поверхность параллельным пучкам, то
т.е. бесконечно удаленная точка изображается на постоянном расстоянии f2 . Эта точка F2 называется задним фокусом преломляющей поверхности.
Если а2 = ¥,
то 
F1 - передний фокус, т.е. если светящаяся точка находится в переднем фокусе (слева на расстоянии f1 от вершины), то сопряженная ей точка – на бесконечности.
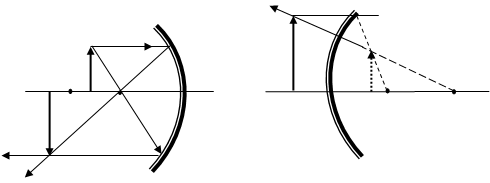
Формула сферического зеркала. Закон преломления легко превратить в закон отражения, если положить формально n2 = - n1 . В этом случае формула преломляющейся поверхности (1) превращается в формулу сферического зеркала (рис.2).
 |
Y Y
C F Y' F C
Y'
Рис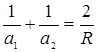. 2
(2)
Видно, что передний и задний фокусы зеркала совпадают, а фокусное расстояние равно половине радиуса. Если обозначить 
, то формула сферического зеркала будет иметь вид:
.
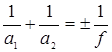Для вогнутого зеркала f > 0, для выпуклого f < 0 (фокус мнимый).
--> ЧИТАТЬ ПОЛНОСТЬЮ <--