Лабораторная работа: Определение момента инерции твердых тел 3

I =Σmiri².

6.2. В каких ситуациях применима теорема Штейнера?

Если известен момент инерции тела относительно любой оси проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера.

6.3. Как формируется теорема Штейнера?

Момент инерции I относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:

I = I0 + ml².

6.4. Под действием какой силы совершается колебательное движение маятника?

Под действием составляющей силы тяжести P1 = Psinφ .

6.5. Является ли момент инерции аддитивной величиной?

Является. Так как к аддитивным величинам относятся масса, энергия, импульс, момент импульса, объем, момент энергии.

6.6. Объяснить метод определения момента инерции с помощью физического маятника.

По основному закону динамики вращательного движения:

M = I∙β = - m∙g∙l∙φ (для малых углов отклонения); так как β = d² φ/dt² , то получаем дифференциальное уравнение гармонических колебаний:

, где ; период колебаний

; отсюда получаем выражение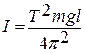

Зная ускорение свободного падения g , массу m , экспериментально измерив l и определив Т , тогда можно вычислить момент инерции маятника .

6.7. Какой маятник называется физическим?

Физическим маятником называется любое твёрдое тело, которое под действием силы тяжести может свободно качаться вокруг неподвижной оси, не проходящей через центр масс.

6.8. При каких формальных допущениях справедлива формула (3,7)?

Период колебаний маятника равен:. Эта формула справедлива когда моментом силы трения можно пренебречь а также силой сопротивления воздуха, так маятник отклоняется на малые углы φ, то допускается sinφ ≈ φ.

6.9. Как записывается основной закон динамики вращательного движения?

Основной закон динамики вращательного движения записывается так: , что является аналитической формой основного уравнения (закона) динамики вращательного движения : при воздействии момента внешних сил твердое тело вращается вокруг неподвижной оси с угловым ускорением, прямо пропорционально моменту сил и обратно пропорционально моменту инерции тела относительно данной оси.