Лабораторная работа: Определение момента инерции твердых тел
где k - константа, зависящая от параметров экспериментальной
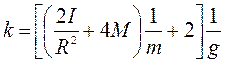 установки:
установки:
(3.8)
где I − его момент инерции блока ;
R – радиус блока ;
M , m – масса груза и перегрузка ;
g – ускорение свободного падения.
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Результаты измерений времени прохождения груза
(Таблица 4.1)
| Номер измерения | h1 =28,0 см | h2 =22,0 см | h3 =18,0 см | h4 =12,0 см | h5 =8,0 см |
| 1 | 3,617 | 3,281 | 3,092 | 2,348 | 1,986 |
| 2 | 3,73 | 3,23 | 2,891 | 2,346 | 1,921 |
| 3 | 3,797 | 3,414 | 3,133 | 2,521 | 2,099 |
| 4 | 3,597 | 3,414 | 3,061 | 2,323 | 2,058 |
| 5 | 3,837 | 3,238 | 2,882 | 2,412 | 2,096 |
| 3,716 | 3,315 | 3,012 | 2,39 | 2,032 | |
| 13,815 | 10,999 | 9,082 | 5,717 | 4,134 |
Из таблицы методического указания к лабораторному практикуму по физике А.Г. Риппа определим коэффициент Стьюдента.
t(a, n ) = 2,1
Расчет погрешностей для построения графиков при коэффициенте
Стьюдента = 2,1
(Таблица 4.2)
| Номер серии опытов | Среднеквадра-тичное отклонение | Случайная погрешность | Абсолютная погрешность | Погрешность
|
| 1 | 0,05 | 0,11 | 0,11 | 13,815 ± 0,8 |
| 2 | 0,04 | 0,08 | 0,08 | 10,999 ± 0,5 |
| 3 | 0,05 | 0,11 | 0,11 | 9,082 ± 0,7 |
| 4 | 0,04 | 0,08 | 0,08 | 5,717 ± 0,4 |
| 5 | 0,04 | 0,08 | 0,08 | 4,134 ± 0,3 |
Определяем абсолютную систематическую приборную погрешность измерения времени согласно методическому указанию к лабораторному практикуму по физике А.Г. Риппа
![]() с.
с.
Построение графиков.
Метод наименьших квадратов для построения прямых по экспериментальным точкам :
![]()
где обозначено:
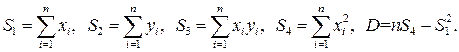
k= 0,49 с2 /м угловой коэффициент прямой
b= 0,06 с2 отрезок, отсекаемый прямой от оси OY
Искомая зависимость имеет вид: t 2 = 0,49∙ h , с2 (4.1)
Вычислим значения ординат прямой линии для двух контрольных точек при произвольных значениях h по выражению 4.1:
h 01 = 15 см, t 2 01 = 0,49×15= 7,35 c2 → точка A 01
h 02 = 29 см, t 2 02 = 0,49×29=14,21 c2 → точка A 02
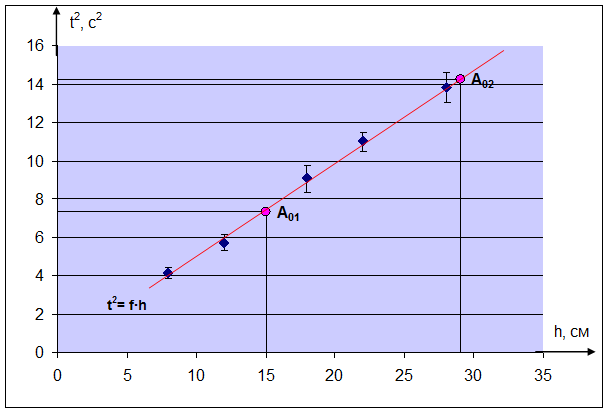
Рисунок 4.1. Зависимость квадрата времени t 2 от пройденного пути h
Погрешности косвенного измерения параметров прямой линии k и b методом наименьших квадратов определяются по следующим формулам:
![]()
где
![]()
∆(k) ≈ 0,01 с2 /м