Лабораторная работа: Решение обыкновенных дифференциальных уравнений
Численное решение строится в форме процедуры Maple, поэтому следует некоторой переменной присвоить результат построения командой dsolve ( ) численного решения в виде процедуры. В дальнейшем имя этой переменной можно использовать как имя процедуры для вычисления значения решения задачи Коши в некоторой точке, соответствующей значению независимой переменной функции решения. Это значение передается в процедуру как ее параметр – после имени процедуры в круглых скобках. Следующий пример демонстрирует построение численного решения задачи Коши и его использование.
> eqn1:=diff(y(x),x$2)+k^2*y(x)=0;
![]()
Переменной f присваиваем результат численного решения задачи Коши для дифференциального уравнения второго порядка (в нулевой точке задается значение неизвестной функции и ее первой производной):
> F:=dsolve({eqn1,y(0)=0,D(y)(0)=1},y(x),type=numeric);
![]()
Если не присвоить параметру k конкретного числового значения, то попытка получить значение решения в точке, например х = 1, приведет к ошибке:
> F(1);
Error, (in dsolve/numeric/rkf45) cannot evaluate boolean: 2.+abs(.2511886433e-1-.2016799760e-5*k^2-.3377712687e-4*k^2*(.2318664400e-1-.3700729218e-5*k^2)+.6309573448e-5*k^2*(.2511886433e-1-.6603721651e-5*k^2)) <= 0.
Следует обязательно определить все символьные параметры дифференциального уравнения числовыми значениями перед использованием численного решения:
> k:=1:
> F(0);F(1);F(2);
![]()
![]()
![]()
Обратите внимание, в каком виде построенная процедура численного решения выдает результаты – в виде списка значений независимой переменной, самой функции и ее производных (до порядка на единицу меньше порядка самого уравнения).
Задачи для самостоятельного решения.
1. Решить уравнения:
1.1. ![]() ; 1.13.
; 1.13. ![]() ;
;
1.2. ![]() ; 1.14.
; 1.14. 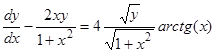 ;
;
1.3. ![]() ; 1.15.
; 1.15. ![]() ;
;
1.4. ![]() ; 1.16.
; 1.16. ![]() ;
;
1.5. ![]() ; 1.17.
; 1.17. ![]() ;
;
1.6. ![]() ; 1.18.
; 1.18. 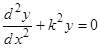 ;
;
1.7. ![]() ; 1.19.
; 1.19. 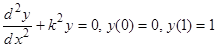 ;
;
1.8. ![]() ; 1.20.
; 1.20. ![]() ;
;
1.9. ![]() ; 1.21.
; 1.21. 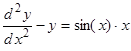 ;
;
1.10. ![]() ; 1.22.
; 1.22. ![]()
1.11. ![]() ; 1.23.
; 1.23. 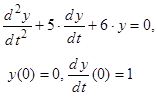 ;
;