Научная работа: Вычисление радиальных функций Матье-Ханкеля
![]() , если
, если ![]() (7)
(7)
![]() , если
, если ![]()
И на бесконечности условию
![]() ~
~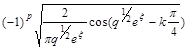 ,
, ![]() (8)
(8)
где ![]() - задано, а
- задано, а ![]() (
(![]() ) - собственные значения задачи (2), (3), (4),
) - собственные значения задачи (2), (3), (4),
![]()
Параметр ![]() используются для различия случаев использования чётного или нечётного номера собственного значения для π и 2π периодических собственных функций:
используются для различия случаев использования чётного или нечётного номера собственного значения для π и 2π периодических собственных функций:

Для решения задачи (6)-(8) используем модификацию метода фазовых функций.
Введём замену переменных:
![]() (9)
(9)
 (10)
(10)
Здесь ![]() - "масштабирующая" функция, положительная на
- "масштабирующая" функция, положительная на ![]() , удовлетворяющая условию
, удовлетворяющая условию ![]() при
при ![]() , её выбор находится в нашем распоряжении.
, её выбор находится в нашем распоряжении.
Подставляя (9), (10) в исходное уравнение (6) задачи для ![]() и
и ![]() :
:
 (11)
(11)
 (12)
(12)
где ![]() и
и ![]() .
.
Для совместного решения задач Коши для ![]() и
и ![]() используется следующий приём. Функцию
используется следующий приём. Функцию ![]() ищем в точках
ищем в точках ![]() . На каждом из отрезков
. На каждом из отрезков ![]() вспомогательные функции
вспомогательные функции ![]() находятся, как решение задач Коши
находятся, как решение задач Коши
![]() (13)
(13)
где ![]() .
.
Поскольку для любых решений ![]() и
и ![]() , уравнений (12) и (13) справедливо соотношение
, уравнений (12) и (13) справедливо соотношение ![]() , получаем рекуррентные формулы «назад» для вычисления
, получаем рекуррентные формулы «назад» для вычисления ![]() ,
, ![]() ,
,
![]() ,
, ![]() , (14)
, (14)
причём ![]() .
.
Итак, краткий алгоритм решения задачи (6)-(8) состоит в следующем:
1. Решаются совместно задачи Коши (11), (12) запоминая в точках разбиения отрезка ![]() величины
величины ![]() ,
, ![]() ,
, ![]() ;
;
2. Полагая ![]() , по формуле (14) вычисляем
, по формуле (14) вычисляем ![]() ,
, ![]() ;
;
3. По формуле (10) вычисляем функции ![]() ,
, ![]() ;
;
4. Из (9) и (10) получаем выражение для производной функции ![]()
![]() .
.