Реферат: Алгебра и топология

Один из общих критериев метризуемости, основанный на концепции локальной конечности, формируется так: пространство C метризуемо в том и только в том случае, если оно регулярно и обладает базой, распадающейся на счетное множество локально конечных семейств множеств.

Регулярным пространством называется топологическое пространство, в котором для каждой точки x и каждого не содержащего ее замкнутого множества A найдутся непересекающиеся множества B и C такие, что xÎB и AÎC.

Локально конечное семейств F множеств – такое семейство, что у каждой точки пространства C есть окрестность, пересекающаяся лишь с конечным множеством его элементов.

Класс метрических пространств внутренним образом связан с классом метризуемых пространств. В этой связи следует отметить, что метрика индуцирует (порождает) топологию и две метрики эквивалентны, если они индуцируют одну и ту же топологию.

Расстояние между точками можно использовать для определения расстояния между точкой и множеством.

Расстояние (x, A) от точки xдо множества А в метрическом пространстве {C, } определяется как inf{(x, y) |yÎA}. Точка x объявляется абсолютно близкой ко множеству A, если (x, A)=0.

Замыканием [A] множества А в {C, } называется множество всех точек из C, абсолютно близких к А. Однозначно отвечающая этой операции топология на множестве C и называется топологией, порожденной на Cметрикой .

Различные варианты метрик приведены в примере 5.3.

Важным подклассом метрических пространств, связанным с теорией алгоритмов, являются эффективно метрические пространства . Это метрические пространства, рассматриваемые вместе с некоторой своей нумерацией, причем требуется, чтобы расстояние между любыми двумя точками этого пространства были вычисленными дистрибутивными числами и существовал алгоритм , дающий программу вычисления такого числа по номерам точек (отсюда и термин вычислимые числа).

Числовой нумерацией множества А называется произвольное отображение f произвольного множества QÌN; если при этом f(q)=a, то q называется f-номером , или просто номером , элемента а (aÎA и qÎQ).

Множество Q-основание или номерное множество нумерации f. Если Q=N, нумерация является натуральной (простой ).

Нумерация называется разрешимой , если существует алгоритм, который применим к любой паре элементов из Q и дает ответ на вопрос, являются ли они или нет номерами одного и того же элемента из А.

Если каждый элемент А имеет только один номер (то есть f – взаимно однозначное соответствие), нумерация называется однозначной (без повторений ) нумерацией .

Пример 5.4. Рассмотрим множество V'u слов русского языка на основе русского алфавита А={Æ, а, б, в, …, ю, я} (|A|=32 буквы, включая пробел, обозначенный знаком Æ).

Один из примитивных методов кодирования слов uÎV является нумерация множества А букв алфавита числами натурального ряда N. Нетрудно увидеть, что в этом случае QÌN, если Q есть множество из каких-то тридцати двух чисел. Например, отображение на рисунке 5.1.

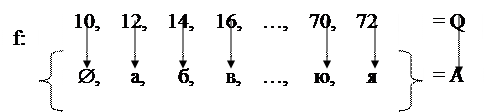4.1. Рис. 5.1.

Если будут нумероваться не только буквы алфавита, но и все образованные слова в каком-то порядке, считая в этом случае и буквы как однобуквенные слова, то Q=N. Номер очередного слова может определяться в соответствии с лексикографическим порядком (см. §1.2, п. 2). Очевидно, что в этом случае будем иметь соответствие g(q)=u, где u некоторое слово из множества слов V, и однозначную нумерацию.

Такого рода процедуру называют иногда арифметизацией . Введенные какие-либо достаточно простые отображения f или g позволяют перевести отношения и операции, определенные на словах, в отношения и операции на номерах. Требование «достаточной простоты» отображения сводятся к тому, чтобы некоторые основные отношения (такие, как отношение вхождения одного слова в другое, – например, вхождение слова «уда», – приспособление для ужения, – в слово на|уда|чу, и т. п.) и операции (такие, как операции соединения слов и т. п.) переходили в отношения и операции, имеющие простую алгоритмическую природу (см. дополнительно §3.3).

2. Линейные (векторные) и нормированные (банаховы) пространства в контексте теории дискретных структур представляют наибольший интерес.

Векторное (линейное) пространство над полем F – аддитивно записанная абелева группа V, в которой определено умножение на скаляр, то есть отображение F´V®V:(l,x)®lx, удовлетворяющее следующим аксиомам (x, yÎV; l, m, 1ÎF):

1) l(x+y) = lx+ly,

2)

(5.2)

(l+m)x = lx+mx,

3) (lm)x = l(mx),

4) 1×x = x

Элементы векторного пространства называются точками этого пространства либо векторами, а элементы поля F – скалярами.

Векторное пространство V есть частный случай модуля над кольцом, а именно, V есть унитарный модуль (модуль с единицей) над полем. Унитарный модуль над некоммутативным телом также называют векторным пространством над телом .

Аксиомы (4.48) отражают аддитивность и однородность линейного пространства.

Пример5.5. К числу линейных пространств относятся:

1. Множество вещественных чисел R с обычно определенными операциями сложения и умножения.

2. Множество всех упорядоченных n-к вещественных чисел, если операции сложения и умножения на число определены следующим образом.

Если x=(x₁ , …, x_n ), y=( y₁ , …, y_n ), то x+y=(x₁ +y₁ , …, x_n +y_n );

при x, yÎR .

3. Пространство функций .Если для любых f(x), g(x)Î под f(x)+g(x) понимается сумма значений f и g, взятые при одних и тех же значениях x. То под lf(x) нужно понимать новую функцию, полученную из f(x) умножением всех ее значений на l. Нулевой функцией будет f(x)=0 на всем отрезке [a,b].

Линейное пространство получает законченное описание тогда, когда свойства аддитивности и однородности дополнены возможностью измерения величин самих элементов (векторов). Введение к понятию линейного нормированного пространства (банахова пространства) , если для каждого xÎX существует неотрицательное число , называемое нормой x. Норма должна удовлетворять следующим условиям:

1) =0 тогда и только тогда, когда x=0;

2) ;

3) – неравенство треугольника.

В этом случае величина обладает всеми свойствами меры (x, y). Действительно:

1) =0, если x-y=0, то есть x=y;

2) =;

3) учитывая, что y-x=-(x-y), находим .

Следовательно, линейное нормированное пространство является метрическим пространством с метрикой

(5.3).

Все рассмотренные ранее метрические пространства дополненные свойствами аддитивности и однородности, превращаются в нормированные линейные пространства. Для этих пространств обычно используют специальные обозначения.

Пример 5.6.

1. Пространство или с нормой 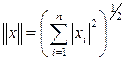при n=1 ;

2. Пространство с нормой ;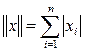

3. Пространство с нормой ;

4. Пространство непрерывных функций f(t), определенных на промежутке [a,b], с нормой .

3. Дискретные пространства и пространства близости . Тривиальное замыкание, определенное ранее, удовлетворяет всем пяти условиям (см. §5.1, п. 2) и, следовательно, является топологией. Эта топология называется дискретной . Все подмножества множества X будут в этой топологии и замкнутыми, и открытыми. Всякое множество может рассматриваться как дискретное топологическое пространство , причем в конечных множествах, где всякое подмножество является объединением конечного числа элементов, возможна лишь дискретная топология.

Пример 5.7.

1. Если семейство U совпадает с множеством B(X) всех подмножеств X (см. §1.1, п.3), то имеет место дискретная топология.

2. Дискретная топология индуцируется тривиальной метрикой (см. Пример 5.3 ):

.

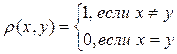В этом случае имеем дискретное топологическое пространство (X, ).

Пример 5.8.

1. Если U ={Æ,X} – крайний случай совокупности U , – то такое семейство определяет топологию на любом множестве X. Такая топология называется антидискретной .

2. Простым примером не дискретного топологического пространства служит прямая линия. Рассматривая ее как числовую прямую и определяя для каждого подмножества A, замыкание как совокупность чисел, являющихся пределами сходящихся последовательностей чисел из A, – получаем топологию, называемую естественно топологией . Одной из полных систем окрестностей здесь служит система всех (открытых) интервалов.

Пространство близости – множество X с бинарным отношением d на множестве всех его подмножеств, удовлетворяющее следующим аксиомам:

1) AdB равносильно BdA (симметричность);

2) Ad(BÈC) равносильно AdB или AdC (аддитивность);

3) AdA равносильно A¹Æ (рефлексивность).

Отношение d определяет близостную структуру, или просто близость на X. При этом, если AdB, то A и B называются близкими множествами, а если (означает отрицание d), – то далекими .

Свойства близости пространства являются обобщением равномерных свойств метрического пространства аналогично тому, как в топологическом пространстве обобщаются его непрерывные свойства.

Понятие близостного пространства представляется полезным в решении проблем метризации путем равномерных покрытий множеств.

Покрытием данного топологического пространства называется любая конечная совокупность его открытых множеств, дающих в своей сумме все это пространство. К числу важных покрытий, тесно связанных с покрытием Лебега размерности, относится e -покрытие отличительной особенностью которого является то, что все его элементы имеют диаметр <e.

Лебега размерность и является той размерностью, которая определяется путем покрытий.

Взаимно однозначное отображение f множества X на множество Y называется близостным изоморфизмом относительно близостей на множествах X и Y. Соответственно, если f близостно непрерывно относительно и обратное отображение f^–1 близостно непрерывно относительно . Близостный изоморфизм есть гомоморфизм индуцированных топологических пространств.

Два пространства близости (X, d) и (Y, ) близостно изоморфны , если существует близостный изоморфизм (X, d) и (Y,). Изучение близостных инвариантов является содержанием теории пространства близости. Каждый топологический инвариант является близостным инвариантом.

Пример 5.9. Каждая метрика порождает близость d на множестве X. Два множества A, BÌX близки относительно d в том и только в том случае, если (A, B)=0. Следовательно, если – произвольная метрика на множестве X и положим AdB тогда и только тогда, когда (A, B)=0, то тем самым определяется близость d на множестве X. Близость d называется близостью индуцированной метрики .

4. Метрика Хемминга – имеет своим истоком проблемы кодирование теории информационных процессов. Основой данной метрики является метрика нормированных множеств булевой алгебры (см. п. 5, примера 5.3).

При формировании метрики Хемминга рассматривается векторное пространство над конечным полем характеристики 2–F₂ , то есть двоичные векторы, как частично упорядоченный набор нулей и единиц (см., например §2.2, п. 8).

Метрикой (расстоянием) Хемминга d между двумя векторами (словами, кодами и т. п.) является число мест, в которых символы двоичных векторов не совпадают.

Пример 5.10. Пусть из всего множества возможных векторов, состоящих из n=8 символов 0 и 1, выбраны векторы-коды слов: a_i , a_j и a_k . Получим расстояние между ними в соответствие с приведенным определением:

ai =	|| 0 1 1 0 1 0 1 1 ||
aj =	|| 1 0 1 0 0 1 1 0 ||
|ai -aj |	* * * * *	d(ai -aj )=5
ak =	|| 0 1 1 0 1 0 1 0||
|ai -ak |	*	d(ai -ak )=1
|aj -ak |	* * * *	d(aj -ak )=4.

Нетрудно проверить, что метрика Хемминга удовлетворяет всем аксиомам расстояния:

1) d(a_i ,a_j )³0 и d(a_i ,a_j )=0, тогда и только тогда, когда a_i =a_j ;

2) d(a_i ,a_j )+d(a_j ,a_k )³d(a_i ,a_k ) (в приведенном примере 5+4>1; заметим также d(a_i ,a_j )+d(a_i ,a_k )³d(a_j ,a_k ) – (5+1>4) и d(a_i ,a_k )+d(a_j ,a_k )=d(a_i ,a_j ) – 1+4=5);

3) d(a_i ,a_j )= d(a_j ,a_i ).

В отдельных случаях может представлять интерес так называемое приведенное расстояние Хемминга – представляющее собой отношение расстояния dkn – размерности пространства.

Пример 5.10.а. Для кодовых слов a_i , a_j и a_k из примера 5.10 относительное расстояние d₁ будет (a_i ,a_j )==0,625, (a_i ,a_k )=0,125 и (a_j ,a_k )=0,5.

5. Примеры метризации. Метрика Хемминга может быть использована в различных задачах. Так в теории систем существует проблема оценки близости подпространства A, BÌX при оценке качеств систем одного и того же назначения. В исходной постановке эту проблему иллюстрирует пример 5.11.

Пример 5.11 . Пусть имеется несколько систем A₁ ,…,A,…,A_m (), каждая из которых обладает своим набором полезных свойств из некоторого полезного набора качеств системы. Строго говоря, полезный набор, чаще всего, определить трудно.

Здесь возможны следующие варианты: