Реферат: Алгебра и топология
2. Различное число свойств 
при одинаковой их «значимости». Естественно, выбирается та система (×), которая имеет большее количество полезных свойств 
.
При наличии нескольких одинаковых по количеству свойств систем – сокращается число систем, принимаемых во внимание.
3. Количество свойств в наборах одинаково, но их составы различны. Здесь может быть полезным использование метрики Хемминга. Так, применяя, например, таблицу «системы – свойства» (см. таблицу 5.1)решение можно получить на основе логической близости по расстоянию Хемминга между мажорантой функцией по составу свойств рассматриваемых систем и булевыми функциями свойств этих систем.
В таблице 5.1 учитываются лишь четыре системы A1 ,A2 ,A3 ,A4 (
). При этом каждая из систем обладает четырьмя из n=8 возможных свойств.
Таблица 5.1.
Системы | X1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | ××× |
| A1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| A2 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | |
| A3 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | |
| A4 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
 | 0 | * | 0 | * | 0 | 0 | * | 0 | |
 | * | 0 | 0 | * | * | 0 | 0 | 0 | |
 | 0 | 0 | 0 | 0 | 0 | * | 0 | 0 | |
 | 0 | 0 | * | 0 | 0 | * | 0 | * |
СвойстваЗдесь «1» – наличие, «0» – отсутствие свойства.
Определение расстояния Хемминга векторами пространства свойств систем A1 ,A2 ,A3 и A4 и функцией показывает, что лучшим приближением к набору наиболее «проявленных» свойств является система A3 .
В теории дискретных структур используется иногда понятие обобщенная метрика Хемминга . Смысл обобщения состоит в распространении оценки расстояния и на нечеткие множества. Последнее означает (см §4.3, п.1) введение вместо дискретной функции принадлежности m(x)={0,1} («не принадлежит» рассматриваемому множеству –0, «принадлежит» – 1) функции принадлежности m(x), определенной на множестве рациональных чисел, обычно на отрезке m(x)=[0,1].
С формальной стороны такое «обобщение» переводит метрику Хемминга в общеизвестную форму линейной метрики (см. пример 5.3, п.2). В самом деле,
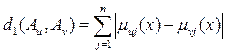
(5.4),
подобна 
(x, y) в п. 2 примера 5.3.
Представляется, что тонкость состоит в том, что фактически вводится в метрику некоторая функция-множитель – в данном случае характеристическая функция принад