Реферат: Анализ и синтез систем автоматического управления и исследование нелинейной системы
D-разбиение в плоскости одного параметра выполняется исходя из условия равенства нулю действительной части характеристического уравнения (полюс на мнимой оси, что соответствует колебательной границе устойчивости системы). Однако, для наглядности представления, график D-разбиения строится на комплексной плоскости. Также, для удобства и наглядности, при построении D-разбиения, учитывают как положительные, так и отрицательные значения частот.
В данном случае, характеристическое уравнение решается относительно коэффициента усиления k:
Действительная часть:
Мнимая часть:
На графике D-разбиения наносится штриховка в сторону устойчивой области.
Рисунок 1.3.5.1 — D-разбиение
Таблица 1.3.5.1 — Данные для построения D-разбиения
| ω | 0 | 2 | 10 | 15 | 20 | 25 | 30 | 40 | 45 | 50 | 60 |
| Ud (ω) | -10 | -8 | -2 | 8 | 22 | 40 | 62 | 118 | 152 | 190 | 278 |
| Vd (ω) | 0 | -8.88 | -17.04 | -23.76 | -28.3 | -30 | -28.1 | -10.56 | 6.48 | 30 | 99.4 |
Как видно, вся плоскость по параметру K разбивается на три зоны, разделяемые точками на оси Ud (ω) с абсциссами:
Первая область — (–∞ ; –10);
вторая область — (–10 ; 190,666667);
третья область — (190,666667 ; +∞).
Так как исходный коэффициент усиления системы, равный 10, находится во второй области устойчивости, можно заключить, что это — область, в которой данная САУ будет устойчива, и штриховку вдоль кривой, описанной графиком D-разбиения, следует нанести в сторону этой области.
1.4 Построение переходного процесса системы методом трапеций
Выполняем построение вещественной частотной характеристики замкнутой системы (рис. 1.4.1).
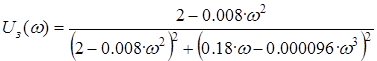
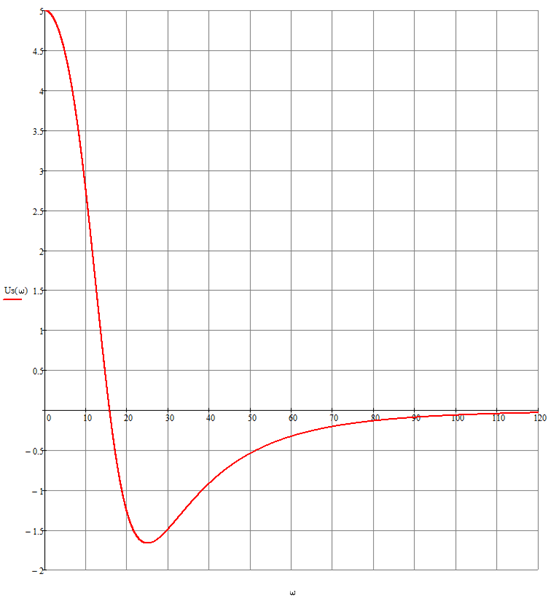
Рисунок 1.4.1 — ВЧХ замкнутой САУ.
Таблица 1.4.1 — Данные для построения АФЧХ замкнутой системы
| ω | 0 | 2 | 10 | 21 | 25 | 30 | 50 | 70 | 100 | 120 |
| Uз (ω) | 5 | 4.92 | 2.76 | -1.43 | -1.67 | -1.49 | -0,54 | -0,21 | -0.64 | -0.034 |
Разбиваем ВЧХ на три трапеции.
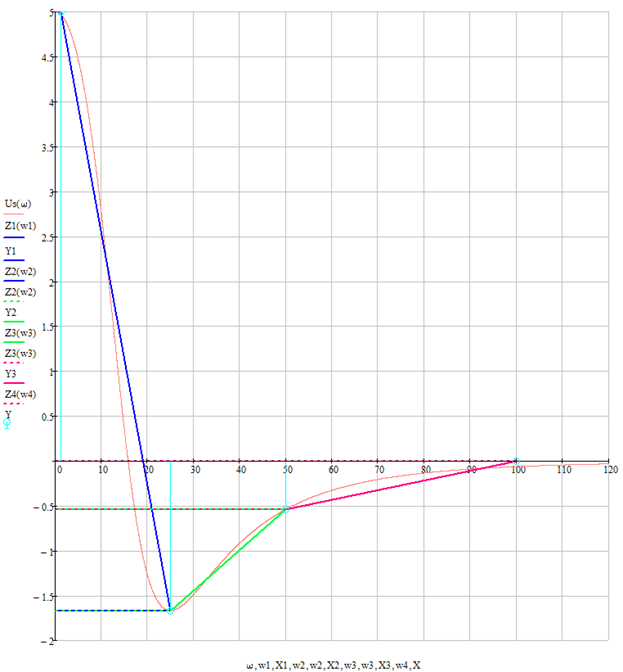
Рисунок 1.4.2 — Разбивка ВЧХ на трапеции.
Синим цветом выделен контур первой трапеция, зелёным – второй, розовым – третьей.
Определяем параметры трапеций: высоту и частоты начала и окончания наклонной стороны (
и 
соответственно).
Для наглядности, совместим трапеции основаниями с осью частот.
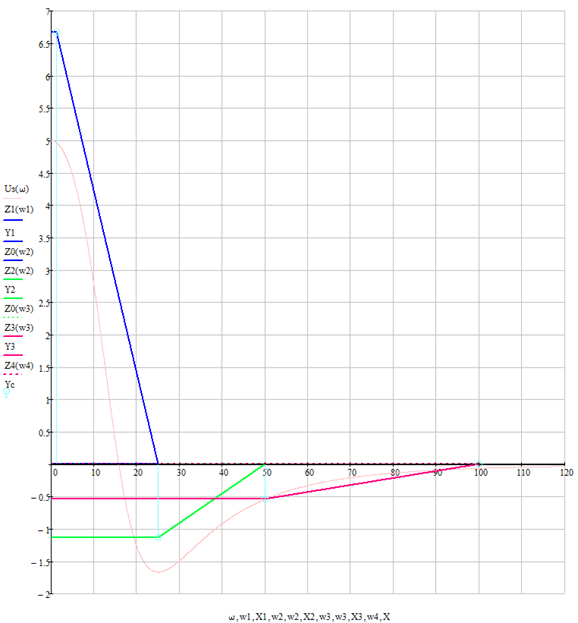
Рисунок 1.4.3 — Трапеции, совмещённые по оси частот.
На основании полученных результатов, строим таблицу.
Таблица 1.4.2 — Параметры трапеций
| 1 трапеция | 2 трапеция | 3 трапеция | |||||||||
| Wd = | 1.25 | Wп = | 25 | Wd = | 25 | Wп = | 50 | Wd = | 50 | Wп = | 100 |
| Х = | 0,05 | R0 = | 6.67 | Х = | 0,5 | R0 = | -1.13 | Х = | 0,50 | R0 = | -0,54 |
В таблице h -функций находим соответствующую каждому 
функцию 
. Искомую составляющую 
получаем из этой функции путём умножения ординат 
на величину 
. Время 
получаем как частное от деления величины 
на 
. 
;
.
Таблица 1.4.3 — Значения для построения переходного процесса.
| t табл, | h табл, | t | h1(t) | t табл, | h табл, | t | h2(t) | t табл, | h табл, | t | h2(t) |
| 0 | 0,0000 | 0,0000 | 0,0000 | 0 | 0,0000 | 0,0000 | 0,0000 | 0 | 0,0000 | 0,0000 | 0,0000 |
| 0,5 | 0,1760 | 0,0200 | 1,1733 | 0,5 | 0,2400 | 0,0100 | -0,2704 | 0,5 | 0,2400 | 0,0050 | -0,1296 |
| 1 | 0,3400 | 0,0400 | 2,2667 | 1 | 0,4610 | 0,0200 | -0,5194 | 1 | 0,4610 | 0,0100 | -0,2489 |
| 1,5 | 0,4940 | 0,0600 | 3,2933 | 1,5 | 0,6650 | 0,0300 | -0,7492 | 1,5 | 0,6650 | 0,0150 | -0,3591 |
| 2 | 0,6280 | 0,0800 | 4,1867 | 2 | 0,8330 | 0,0400 | -0,9385 | 2 | 0,8330 | 0,0200 | -0,4498 |
| 2,5 | 0,7390 | 0,1000 | 4,9267 | 2,5 | 0,9670 | 0,0500 | -1,0895 | 2,5 | 0,9670 | 0,0250 | -0,5222 |
| 3 | 0,8280 | 0,1200 | 5,5200 | 3 | 1,0610 | 0,0600 | -1,1954 | 3 | 1,0610 | 0,0300 | -0,5729 |
| 3,5 | 0,8920 | 0,1400 | 5,9467 | 3,5 | 1,1150 | 0,0700 | -1,2562 | 3,5 | 1,1150 | 0,0350 | -0,6021 |
| 4 | 0,9380 | 0,1600 | 6,2533 | 4 | 1,1420 | 0,0800 | -1,2867 | 4 | 1,1420 | 0,0400 | -0,6167 |
| 4,5 | 0,9600 | 0,1800 | 6,4000 | 4,5 | 1,1380 | 0,0900 | -1,2821 | 4,5 | 1,1380 | 0,0450 | -0,6145 |
| 5 | 0,9770 | 0,2000 | 6,5133 | 5 | 1,1170 | 0,1000 | -1,2585 | 5 | 1,1170 | 0,0500 | -0,6032 |
| 5,5 | 0,9860 | 0,2200 | 6,5733 | 5,5 | 1,0920 | 0,1100 | -1,2303 | 5,5 | 1,0920 | 0,0550 | -0,5897 |
| 6 | 0,9820 | 0,2400 | 6,5467 | 6 | 1,0510 | 0,1200 | -1,1841 | 6 | 1,0510 | 0,0600 | -0,5675 |
| 6,5 | 0,9800 | 0,2600 | 6,5333 | 6,5 | 1,0180 | 0,1300 | -1,1469 | 6,5 | 1,0180 | 0,0650 | -0,5497 |
| 7 | 0,9790 | 0,2800 | 6,5267 | 7 | 0,9930 | 0,1400 | -1,1188 | 7 | 0,9930 | 0,0700 | -0,5362 |
| 7,5 | 0,9800 | 0,3000 | 6,5333 | 7,5 | 0,9740 | 0,1500 | -1,0974 | 7,5 | 0,9740 | 0,0750 | -0,5260 |
| 8 | 0,9850 | 0,3200 | 6,5667 | 8 | 0,9660 | 0,1600 | -1,0884 | 8 | 0,9660 | 0,0800 | -0,5216 |
| 8,5 | 0,9890 | 0,3400 | 6,5933 | 8,5 | 0,9660 | 0,1700 | -1,0884 | 8,5 | 0,9660 | 0,0850 | -0,5216 |
| 9 | 0,9970 | 0,3600 | 6,6467 | 9 | 0,9700 | 0,1800 | -1,0929 | 9 | 0,9700 | 0,0900 | -0,5238 |
| 9,5 | 1,0040 | 0,3800 | 6,6933 | 9,5 | 0,9750 | 0,1900 | -1,0985 | 9,5 | 0,9750 | 0,0950 | -0,5265 |
| 10 | 1,0090 | 0,4000 | 6,7267 | 10 | 0,9820 | 0,2000 | -1,1064 | 10 | 0,9820 | 0,1000 | -0,5303 |
| 10,5 | 1,0130 | 0,4200 | 6,7533 | 10,5 | 0,9870 | 0,2100 | -1,1120 | 10,5 | 0,9870 | 0,1050 | -0,5330 |
| 11 | 1,0150 | 0,4400 | 6,7667 | 11 | 0,9970 | 0,2200 | -1,1233 | 11 | 0,9970 | 0,1100 | -0,5384 |
| 11,5 | 1,0160 | 0,4600 | 6,7733 | 11,5 | 0,9970 | 0,2300 | -1,1233 | 11,5 | 0,9970 | 0,1150 | -0,5384 |
| 12 | 1,0150 | 0,4800 | 6,7667 | 12 | 0,9970 | 0,2400 | -1,1233 | 12 | 0,9970 | 0,1200 | -0,5384 |
| 12,5 | 1,0130 | 0,5000 | 6,7533 | 12,5 | 0,9970 | 0,2500 | -1,1233 | 12,5 | 0,9970 | 0,1250 | -0,5384 |
| 13 | 1,0120 | 0,5200 | 6,7467 | 13 | 0,9970 | 0,2600 | -1,1233 | 13 | 0,9970 | 0,1300 | -0,5384 |
| 13,5 | 1,0110 | 0,5400 | 6,7400 | 13,5 | К-во Просмотров: 222
Бесплатно скачать Реферат: Анализ и синтез систем автоматического управления и исследование нелинейной системы
|