Реферат: Анализ качественных характеристик следящей системы
Если ошибка имеет конечное установившееся значение, для ее оценки используют теорию преобразований Лапласа, в частности, теорему о предельном значении оригинала:
![]() ,
,
где ![]() ;
; ![]() - передаточная функция от воздействия к ошибке.
- передаточная функция от воздействия к ошибке.
Если ошибка изменяется с течением времени, для ее расчета используется метод разложения ошибки по производным входного воздействия. Рассмотрим этот метод.
Величина ![]() может быть определена с помощью интеграла свертки:
может быть определена с помощью интеграла свертки:
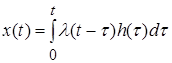 . (3)
. (3)
Передаточная функция связана с весовой функцией преобразованием Лапласа:
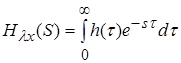 . (4)
. (4)
Представим задающее воздействие степенным рядом с ограниченным числом членов:
![]()
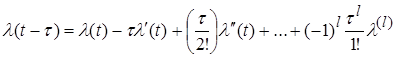 . (5)
. (5)
Подставив формулу (5) в (3), получим:
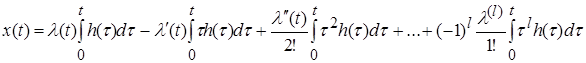 . (6)
. (6)
Если ![]() (
(![]() ─ длительность переходного процесса), то в этом случае
─ длительность переходного процесса), то в этом случае ![]() и можно заменить верхний предел интегралов в (6) на бесконечность, поскольку увеличение предела не изменяет значения интеграла. Тогда (5.6) можно записать в виде:
и можно заменить верхний предел интегралов в (6) на бесконечность, поскольку увеличение предела не изменяет значения интеграла. Тогда (5.6) можно записать в виде:
![]() , (7)
, (7)
где ![]() – коэффициенты ошибки:
– коэффициенты ошибки:
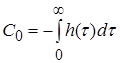 ;
; 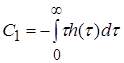 ;
; 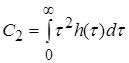 ;
; 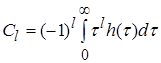 .
.
![]() - коэффициент ошибки по положению;
- коэффициент ошибки по положению;
![]() - коэффициент ошибки по скорости;
- коэффициент ошибки по скорости;
![]() - коэффициент ошибки по ускорению;
- коэффициент ошибки по ускорению;
![]() - коэффициент ошибки по l-ой производной входного воздействия.
- коэффициент ошибки по l-ой производной входного воздействия.
![]() - ошибка по положению;
- ошибка по положению; ![]() - ошибка по скорости;
- ошибка по скорости;
![]() - ошибка по ускорению.
- ошибка по ускорению.
Нетрудно видеть, что
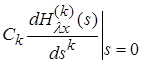 .
.
Понятие астатизма системы
С величиной коэффициентов ошибки связано понятие астатизма системы.
Порядок астатизма системы определяется индексом первого, отличного от нуля коэффициента ошибки. Если ![]() система обладает астатизмом 0-го порядка и называется статической, если
система обладает астатизмом 0-го порядка и называется статической, если ![]() ;
; ![]() ─ система обладает астатизмом 1-го порядка.
─ система обладает астатизмом 1-го порядка.
![]() ;
; ![]() ;
; ![]() - система с астатизмом 2-го порядка и т.д.
- система с астатизмом 2-го порядка и т.д.
Астатические системы обладают следующим свойством: если на вход системы с астатизмом k-го порядка подается входное воздействие, описываемое полиномом k-ой степени, значение ошибки в установившемся режиме постоянно и не равно нулю.
Если порядок астатизма больше степени полинома, установившееся значение ошибки равно нулю (![]() ). Если порядок астатизма меньше степени полинома, определяющего задающее воздействие, ошибка изменяется с течением времени и в пределе будет равна бесконечности.
). Если порядок астатизма меньше степени полинома, определяющего задающее воздействие, ошибка изменяется с течением времени и в пределе будет равна бесконечности.