Реферат: Анализ качественных характеристик следящей системы

Порядок астатизма также зависит от точки приложения воздействия (рис.3).

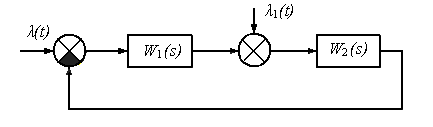
Рис.3. К определению порядка астатизма системы.

Если астатизм определяется по отношению к воздействию , то его порядок определяется суммой интегрирующих звеньев в (s) и (s).

Относительно порядок астатизма определяется числом интегрирующих звеньев в (s) и не зависит от их числа в (s). Соответствующие передаточные функции, связывающие задающее воздействие и ошибку слежения, определяются выражениями

; .

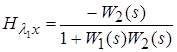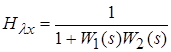Таким образом, порядок астатизма системы определяется числом интегрирующих звеньев, включенных в цепь обратной связи между точкой приложения воздействия и точкой измерения ошибки слежения.

Методы вычисления коэффициентов ошибки

Представим передаточную функцию в виде

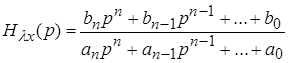. (8);

В разложении ошибки по производным входного воздействия

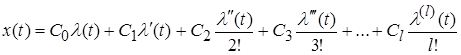
заменим операцию дифференцирования символом р, т.е. = pи вынесем формально общий множитель за скобки:

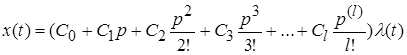(9);

С другой стороны можно определить дифференциальным уравнением, записанным в сокращенной форме:

. (10)

Подставив (8) в (10), приравняем выражения (9) и (10) 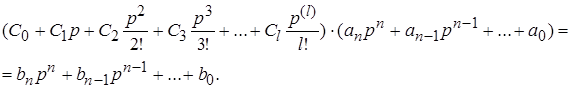(5.11)

Приравняв слагаемые, имеющие одинаковые степени р в правой и левой частях (11), получим:

; ;

;

; .

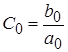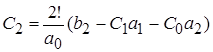На основании полученных выражений можно записать формулу для расчета коэффициентов ошибки:

. (12)

Коэффициенты ошибки могут быть также вычислены по формулам, составленным из коэффициентов полиномов числителя и знаменателя передаточной функции разомкнутой системы:

, (13)

где k – добротность системы; v – порядок астатизма.

Приведенные в табл.1 формулы получены по вышеизложенной методике подстановкой в выражение

передаточной функции разомкнутой системы в виде (13).