Реферат: Анализ производственных функций

что совершенно естественно: недостаток труда можно компенсировать его лучшей фондовооруженностью.

Изоклиналями называются линии наибольшего роста ПФ. Изокли­нали ортогональны линиям нулевого роста, т.е. изоквантам. Поскольку направление наибольшего роста в каждой точке (К, L) задается градиентом

grad , то уравнение изоклинали записывается в форме

В частности, для мультипликативной ПФ получаем,

поэтому изоклиналь задается дифференциальным уравнением,

, которое имеет решение

,

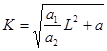где ( L₀ ; К ₀ ) - координаты точки, через которую проходит изоклиналь. Наиболее простая изоклиналь при а = 0 представляет собой прямую

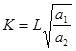
На рис. 1 изображены изокванты и изоклинали мультипликатив­ной ПФ.

При изучении факторов роста экономики выделяют экстенсивные факторы роста (за счет увеличения затрат ресурсов, т.е. увеличения масштаба производства) и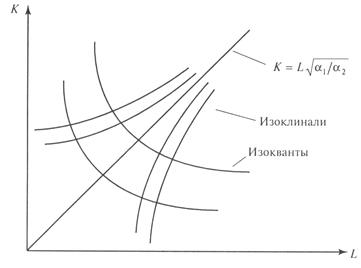

рис. 1

интенсивные факторы роста (за счет повы­шения эффективности использования ресурсов).

Возникает вопрос: как с помощью ПФ выразить масштаб и эффек­тивность производства? Это сравнительно легко сделать, если выпуск и затраты выражены в соизмеримых единицах, например представлены в соизмеримой стоимостной форме. Однако проблема соизмерения на­стоящего и прошлого труда до сих пор не решена удовлетворительным образом. Поэтому воспользуемся переходом к относительным (безраз­мерным) показателям.В относительных показателях мультипликативная ПФ записывается следующим образом:

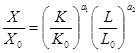
те X₀ , K₀ L₀ — значения выпуска и затрат фондов и труда в базовый год.

Безразмерная форма , указанная выше , легко приводится к первоначальному виду

Таким образом, коэффициент

получает естественную интер­претацию - это коэффициент, который соизмеряет ресурсы с выпуском. Если обозначить выпуск и ресурсы в относительных (безразмер­ных) единицах измерения через x, k, l, то ПФ в форме

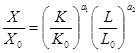
запи­шется так:

Найдем теперь эффективность экономики, представленной ПФ . Напомним, что эффективность — это отношение результата к затратам. В нашем случае два вида затрат: затраты прошлого труда в виде фондов k и настоящего труда l. Поэтому имеются два частныхпоказателя эффективности: -фондоотдача , - производитель труда.

Поскольку частные показатели эффективности имеют одинаковую размерность (точнее, одинаково безразмерны), то можно находить любые средние из них. Так как ПФ выражена в мультипликативной форме, то и среднее естественно взять в такой же форме, т.е. среднегеометриче­ское значение.

Итак, обобщенный показатель экономической эффективности есть взвешенное среднее геометрическое частных показателей экономичес­кой эффективности:

в котором роль весов выполняют относительные эластичности

т.е. частные эффективности участвуют в образовании обобщенной эффективности с такими же приоритетами, с какими входят в ПФ соответствующие ресурсы.

Из вытекает, что с помощью коэффициента экономичес­кой эффективности ПФ преобразуется в форму, внешне совпадающую с функцией Кобба-Дугласа:

k=Ek^a l^1-a

в соотношении с чем Е - не постоянный коэффициент, а функ­ция от (К, L).

Поскольку масштаб производства М проявляется в объеме затрачен­ных ресурсов, то по тем же соображениям, которые были приведены при расчете обобщенного показателя экономической эффективности, сред­ний размер использованных ресурсов (т.е. масштаб производства)

M=k^a l^1-a